题目内容
定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4)时,f(x)=2x,则f(sin1)与f(cos1)的大小关系为( )
| A、f(sin1)<f(cos1) |
| B、f(sin1)=f(cos1) |
| C、f(sin1)>f(cos1) |
| D、不确定 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系即可得到结论.
解答:
解:∵当x∈[3,4)时,f(x)=2x,∴此时函数单调递增,
∵f(x)=f(x+2),∴函数在[-1,0)上单调递增,
∵f(x)是偶函数,∴f(x)在(0,1]上单调递减,
∵0<cos1<sin1<1,
∴f(sin1)<f(cos1),
故选:A
∵f(x)=f(x+2),∴函数在[-1,0)上单调递增,
∵f(x)是偶函数,∴f(x)在(0,1]上单调递减,
∵0<cos1<sin1<1,
∴f(sin1)<f(cos1),
故选:A
点评:本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系,是解决本题的关键.

练习册系列答案
相关题目
定义在R上的函数f(x)=
,若函数g(x)=lna-f(x)有4个不零点,则实数a的取值范围是( )
|
| A、(1,e)∪(e,+∞) | ||
B、(
| ||
C、(
| ||
D、(
|
已知向量
,
,
且满足
+
+
=
,|
|=3,|
|=4,|
|=5,设
与
的夹角为θ1,
与
的夹角为θ2,
与
的夹角为θ3,则它们的大小关系是( )
| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
| A、θ1<θ2<θ3 |
| B、θ1<θ3<θ2 |
| C、θ2<θ3<θ1 |
| D、θ3<θ2<θ1 |
函数f(x)=
sin2x最小值是( )
| 1 |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知x>0,y>0,
+
=1.若x+2y>m2-2m恒成立,则实数m的取值范围是( )
| 2 |
| x |
| 1 |
| y |
| A、m≥4或m≤-2 |
| B、-2<m<4 |
| C、m≥2或m≤-4 |
| D、-4<m<2 |
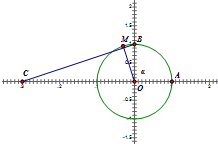 如图,A、B是单位圆与x轴、y轴正半轴的交点,点M在单位圆上,∠AOM=α(0<α<π),点C(-3,0),若BC⊥OM,则sin(2α-
如图,A、B是单位圆与x轴、y轴正半轴的交点,点M在单位圆上,∠AOM=α(0<α<π),点C(-3,0),若BC⊥OM,则sin(2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|