题目内容
定义在R上的函数f(x)=
,若函数g(x)=lna-f(x)有4个不零点,则实数a的取值范围是( )
|
| A、(1,e)∪(e,+∞) | ||
B、(
| ||
C、(
| ||
D、(
|
考点:分段函数的应用
专题:函数的性质及应用
分析:由g(x)=0得lna=f(x),作出函数f(x)的图象,利用数形结合即可得到结论.
解答:
解:由g(x)=lna-f(x)=0,得lna=f(x),
作出函数f(x)的图象如图:
要使函数g(x)=lna-f(x)有4个不零点,
则lna>-1且lna≠1,
即a>
且a≠e,
故选:D
作出函数f(x)的图象如图:

| 1 |
| e |
要使函数g(x)=lna-f(x)有4个不零点,
则lna>-1且lna≠1,
即a>
| 1 |
| e |
故选:D
点评:本题主要考查函数零点的应用,根据函数和方程之间的关系,转化为两个函数交点个数问题以及数形结合是解决本题的关键.

练习册系列答案
相关题目
定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4)时,f(x)=2x,则f(sin1)与f(cos1)的大小关系为( )
| A、f(sin1)<f(cos1) |
| B、f(sin1)=f(cos1) |
| C、f(sin1)>f(cos1) |
| D、不确定 |
下列函数中是幂函数的是( )
| A、y=2x2 | ||
B、y=
| ||
| C、y=x2+x | ||
D、y=-
|
在等比数列{an}中,有a1a5=4,则a3的值为( )
| A、±2 | B、-2 | C、2 | D、4 |
sin225°的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
 关于下列命题:
关于下列命题: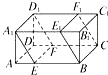 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部份,其体积分别记为V1=VAEA1-DFD1,V2=VEBE1A1-FCF1D1,V3=VB1E1BC1F1C,若V1:V2:V3=1:4:1,则截面A1EFD1的面积为