题目内容
在△ABC中,a=1,b=2,cosC=
,则c= .
| 1 |
| 2 |
考点:余弦定理
专题:解三角形
分析:利用余弦定理列出关系式,将a,b,cosC的值代入即可求出c的值.
解答:
解:∵在△ABC中,a=1,b=2,cosC=
,
∴由余弦定理得:c2=a2+b2-2abcosC=1+4-2=3,
则c=
.
故答案为:
| 1 |
| 2 |
∴由余弦定理得:c2=a2+b2-2abcosC=1+4-2=3,
则c=
| 3 |
故答案为:
| 3 |
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,4)时,f(x)=2x,则f(sin1)与f(cos1)的大小关系为( )
| A、f(sin1)<f(cos1) |
| B、f(sin1)=f(cos1) |
| C、f(sin1)>f(cos1) |
| D、不确定 |
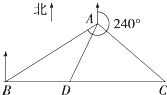 海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10
海上一观测站测得方位角240°的方向上有一艘停止待修的商船,在商船的正东方有一艘海盗船正向它靠近,速度为每小时90海里.此时海盗船距观测站10