题目内容
17.已知F1和F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,O为坐标原点,点P(-1,$\frac{\sqrt{2}}{2}$)在该椭圆上,且PF1⊥x轴.(1)求椭圆的标准方程;
(2)若过点A(2,0)作直线l交椭圆于不同的两点B,C,证明:不存在直线l,使得|BF2|=|CF2|.
分析 (1)通过点P(-1,$\frac{\sqrt{2}}{2}$)在该椭圆上且PF1⊥x轴可知焦点坐标,利用椭圆定义可知a=$\sqrt{2}$,进而计算可得结论;
(2)利用反证法证明,假设满足题意的直线l方程为x=my+2,与椭圆方程联立,结合韦达定理及两点间距离公式化简可知当|BF2|=|CF2|时有m(4+3m2)=0,从而得出结论.
解答 (1)解:∵点P(-1,$\frac{\sqrt{2}}{2}$)在该椭圆上,且PF1⊥x轴,
∴椭圆方程焦点为(-1,0),(1,0),
2a=|PF1|+|PF2|=$\frac{\sqrt{2}}{2}$+$\sqrt{(-1-1)^{2}+(\frac{\sqrt{2}}{2})^{2}}$=2$\sqrt{2}$,即a=$\sqrt{2}$,
又∵b2=a2-c2=2-1=1,
∴椭圆的标准方程为:$\frac{{x}^{2}}{2}$+y2=1;
(2)证明: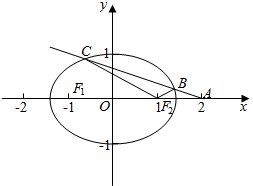 假设过点A(2,0)与椭圆相交的直线l的方程为:x=my+2,
假设过点A(2,0)与椭圆相交的直线l的方程为:x=my+2,
并与椭圆方程联立,消去x整理得:(2+m2)y2+4my+2=0,
设B(x1,y1),C(x2,y2),则y1+y2=$\frac{4m}{2+{m}^{2}}$,y1y2=-$\frac{2}{2+{m}^{2}}$,
∵|BF2|=|CF2|,F2(1,0),
∴$({x}_{1}-1)^{2}$+${{y}_{1}}^{2}$=$({x}_{2}-1)^{2}$+${{y}_{2}}^{2}$,
整理得:(x1-x2)(x1+x2-2)=(y2-y1)(y2+y1),
化简得:(1+m2)(y1+y2)+2m=0,
∴(1+m2)•$\frac{4m}{2+{m}^{2}}$+2m=0,
∴m(4+3m2)=0,
解得:m=0,而此时显然|BF2|≠|CF2|,矛盾,
故不存在直线l,使得|BF2|=|CF2|.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,利用反证法是解决本题的关键,注意解题方法的积累,属于中档题.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | 若直线l平行于平面α内的无数条直线,则l∥α | |
| B. | 若直线a在平面α外,则a∥α | |
| C. | 若直线a∥b,b?α,则a∥α | |
| D. | 若直线a∥b,b?α,则直线a就平行于平面内的无数条直线 |
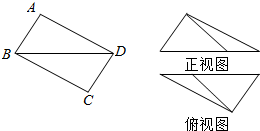 如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )
如图,在矩形ABCD中,$AB=\frac{3}{2},BC=2$,沿BD将矩形ABCD折叠,连接AC,所得三棱锥A-BCD的正视图和俯视图如图所示,则三棱锥A-BCD的侧视图的面积为( )| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{18}{25}$ | D. | $\frac{36}{25}$ |




