题目内容

7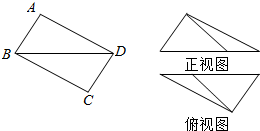．如图，在矩形ABCD中，$AB=\frac{3}{2}，BC=2$，沿BD将矩形ABCD折叠，连接AC，所得三棱锥A-BCD的正视图和俯视图如图所示，则三棱锥A-BCD的侧视图的面积为（　　）
A．$\frac{9}{25}$B．$\frac{12}{5}$C．$\frac{18}{25}$D．$\frac{36}{25}$

分析 由题意可知平面ABD⊥平面BCD，三棱锥A-BCD侧视图为等腰直角三角形，两条直角边分别是过B和D向AC所做的垂线，做出直角边的长度，得到侧视图的面积．

解答 解：由正视图和俯视图可知平面ABD⊥平面BCD．
三棱锥A-BCD侧视图为等腰直角三角形，两条直角边分别是过A和C向BD所做的垂线，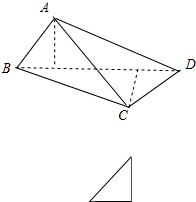

由等面积可得直角边长为$\frac{\frac{3}{2}×2}{\sqrt{（\frac{3}{2}）^{2}+{2}^{2}}}$=$\frac{6}{5}$，
∴侧视图面积为$\frac{1}{2}$×$\frac{6}{5}$×$\frac{6}{5}$=$\frac{18}{25}$．
故选：C

点评 本题考查的知识点是由三视图，求体积和表面积，根据已知的三视图，判断几何体的形状是解答的关键．

练习册系列答案
相关题目
17．已知F1和F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，O为坐标原点，点P（-1，$\frac{\sqrt{2}}{2}$）在该椭圆上，且PF1⊥x轴．
（1）求椭圆的标准方程；
（2）若过点A（2，0）作直线l交椭圆于不同的两点B，C，证明：不存在直线l，使得|BF2|=|CF2|．
18．在△ABC中，角A，B，C所对的边分别为a，b，c，向量$\overrightarrow{m}$=（2，cos2C-1），$\overrightarrow{n}$=（sin2$\frac{A+B}{2}$，1）且$\overrightarrow{m}$⊥$\overrightarrow{n}$．
（1）求角C的大小；
（2）如果△ABC的外接圆的半径为1，求△ABC的面积的最大值．
15．设正数a，b满足log2a=log3b，则下列结论中，不可能成立的是（　　）
A．1＜a＜bB．0＜b＜a＜1C．a=bD．1＜b＜a
2．已知函数$f（x）=2sin（2x+\frac{π}{6}）$．
（Ⅰ）求函数f（x）在区间$[-\frac{π}{6}，\frac{π}{6}]$上的最大值和最小值；
（Ⅱ）求函数f（x）的单调递增区间．
12．已知向量$\overrightarrow{m}$=（$\sqrt{3}$cos$\frac{x}{2}$，cos$\frac{x}{2}$），$\overrightarrow{n}$=（sin$\frac{x}{2}$，cos$\frac{x}{2}$），函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）在锐角△ABC中，已知A=$\frac{π}{3}$，求f（B）的取值范围．
19．等差数列{an}中，a3=7，a5=a2+6，则{an}的通项公式为an=2n+1．
16．己知函数f（x）=x-a1nx（a≠0，a∈R）．
（Ⅰ）讨论f（x）的极值；
（Ⅱ）设A（x1，f（x1）），B（x2，f（x2））（0＜x1＜x2）是曲线y=f（x）上不同两点，若存在t∈（x1，x2），使得y=f（x）在（t，f（t））处的切线与直线AB平行，求证：t＜$\frac{{x}_{1}+{x}_{2}}{2}$．
17．函数f（x）=$\sqrt{sinx-\frac{1}{2}}$，x∈（0，2π）的定义域是[$\frac{π}{6}$，$\frac{5π}{6}$]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网