题目内容
设点P在曲线y=2ex上,点Q在直线y=2x-1上,则|PQ|的最小值为 .
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:设与直线y=2x-1平行的直线y=2x+c与曲线y=2ex相切与点P(x0,y0),两平行线间的距离即为|PQ|的最小值,由相切函数平行线间的距离公式可得.
解答:
解:设与直线y=2x-1平行的直线y=2x+c与曲线y=2ex相切与点P(x0,y0),
则两平行线间的距离即为|PQ|的最小值,
∴2ex0=2,2x0+c=2ex0,解得x0=0,c=2,
∴曲线的切线为y=2x+2,
由平行线间的距离公式可得|PQ|的最小值为
=
故答案为:
则两平行线间的距离即为|PQ|的最小值,
∴2ex0=2,2x0+c=2ex0,解得x0=0,c=2,
∴曲线的切线为y=2x+2,
由平行线间的距离公式可得|PQ|的最小值为
| |-1-2| | ||
|
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |
点评:本题考查指数函数的导数,涉及切线问题,属基础题.

练习册系列答案
相关题目
函数f(x)=x2-
x+
,x∈[0,1],n∈Z的值域中恰好有一个整数,则n的值为( )
| n |
| 2 |
| 1 |
| 2 |
| A、0或1 |
| B、0或2 |
| C、0或1或3或4 |
| D、0或1或2或3 |
已知数列{an}的前n项和为Sn,已知a1=2,且nSn+1-(n+1)Sn=n(n+1)(n∈N+),则过A(n,an)和B(n+2,an+2)的直线的一个方向向量的坐标可以是( )
| A、(2,-4) | ||||
| B、(-1,-1) | ||||
C、(-
| ||||
D、(1,-
|
在(x-y)10的展开式中,系数最小的项是( )
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
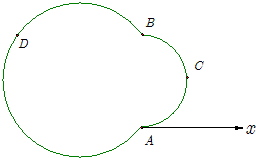 在极坐标系中,极点为A,已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成.已知B(4,
在极坐标系中,极点为A,已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成.已知B(4,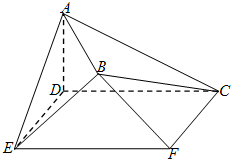 如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=
如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=