题目内容
已知点P的坐标（x，y）满足
，过点P的直线l与圆C：x2+y2=36相交于A、B两点，则弦AB长的最小值为 ．
|
考点：二元一次不等式（组）与平面区域,直线与圆相交的性质
专题：不等式的解法及应用
分析：作出不等式对应的平面区域，利用直线与圆的位置关系，确定点P的位置，进行即可即可．
解答：
解作出不等式对应的平面区域如图（阴影部分CDE），
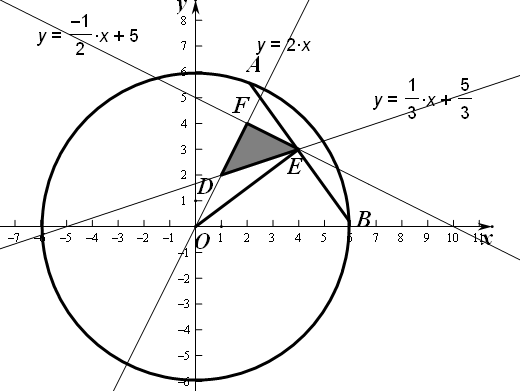
过点P的直线l与圆C：x2+y2=36相交于A、B两点，要使|AB|最小，
则圆心到过P的直线的距离最大，
由图象可知当点P在E处时，满足条件，此时OE⊥AB，E是直线x-3y+5=0与x+2y-10=0的交点，为（4，3），所以OE=5，又OB=6，所以AB=2
=2
；
故答案为：2
．
过点P的直线l与圆C：x2+y2=36相交于A、B两点，要使|AB|最小，
则圆心到过P的直线的距离最大，
由图象可知当点P在E处时，满足条件，此时OE⊥AB，E是直线x-3y+5=0与x+2y-10=0的交点，为（4，3），所以OE=5，又OB=6，所以AB=2
| 62-52 |
| 11 |
故答案为：2
| 11 |
点评：本题主要考查平面区域的画法和直线与圆的位置关系的应用；利用直线和圆相交，根据弦长公式确定点P的位置是解决本题的关键，属于中档题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
如果x∈（-
，0）时总有k（x+
）＞cosx成立，则实数k的取值范围是（ ）
| π |
| 2 |
| π |
| 2 |
| A、（1，+∞） | ||
| B、[1，+∞） | ||
C、(
| ||
D、[
|
设m，n是两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（ ）
| A、若m⊥n，m⊥α，n∥β，则α∥β |
| B、若m∥α，n∥β，α∥β则m∥n |
| C、若m∥n，m∥α，n∥β，则α∥β |
| D、若m⊥α，n∥β，α∥β，则m⊥n |
