题目内容
已知下列四个命题:
①函数f(x)=2x满足:对任意x1、x2∈R且x1≠x2都有f(
)<
[f(x1)+f(x2)];
②函数f(x)=log2(x+
),g(x)=1+
不都是奇函数;
③若函数f(x)满足f(x-1)=-f(x+1),且f(1)=2,则f(7)=-2;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
其中正确命题的序号是 .
①函数f(x)=2x满足:对任意x1、x2∈R且x1≠x2都有f(
| x1+x2 |
| 2 |
| 1 |
| 2 |
②函数f(x)=log2(x+
| 1+x2 |
| 2 |
| 2x-1 |
③若函数f(x)满足f(x-1)=-f(x+1),且f(1)=2,则f(7)=-2;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
其中正确命题的序号是
考点:命题的真假判断与应用
专题:综合题,简易逻辑
分析:对四个命题分别进行判断,即可得出结论.
解答:
解:①函数f(x)=2x是凹函数,对任意x1、x2∈R且x1≠x2都有f(
)<
[f(x1)+f(x2)]成立,故正确;
②f(x)+f(-x)=log2(x+
)+log2(-x+
)=0,∴f(x)=log2(x+
)是奇函数,故②不正确;
③若函数f(x)满足f(x-1)=-f(x+1),则f(x+2)=-f(x),f(x+4)=f(x),∴f(7)=f(-1),
∵f(-1)=-f(1)且f(1)=2,∴f(7)=-2,正确;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
∵|logax|=k(a>0,a≠1),∴logax=±k,∴x1=ak,x2=a-k,则x1x2=ak•a-k=a0=1,∴命题正确;
所以,正确命题的序号是:①③④
故答案为:①③④.
| x1+x2 |
| 2 |
| 1 |
| 2 |
②f(x)+f(-x)=log2(x+
| 1+x2 |
| 1+x2 |
| 1+x2 |
③若函数f(x)满足f(x-1)=-f(x+1),则f(x+2)=-f(x),f(x+4)=f(x),∴f(7)=f(-1),
∵f(-1)=-f(1)且f(1)=2,∴f(7)=-2,正确;
④设x1、x2是关于x的方程|logax|=k(a>0且a≠1)的两根,则x1x2=1,
∵|logax|=k(a>0,a≠1),∴logax=±k,∴x1=ak,x2=a-k,则x1x2=ak•a-k=a0=1,∴命题正确;
所以,正确命题的序号是:①③④
故答案为:①③④.
点评:本题通过命题真假的判定,考查了函数单调的性质与图象的变换以及方程的知识,是容易出错的题目.

练习册系列答案
相关题目
函数f(x)=lnx+x2-4零点所在的大致区间为( )
| A、(1,2) |
| B、(2,3) |
| C、(3,4) |
| D、(4,5) |
函数y=x|x|+px,x∈R是( )
| A、偶函数 |
| B、奇函数 |
| C、即不是奇函数也不是偶函数 |
| D、奇偶性与p有关 |
如果x∈(-
,0)时总有k(x+
)>cosx成立,则实数k的取值范围是( )
| π |
| 2 |
| π |
| 2 |
| A、(1,+∞) | ||
| B、[1,+∞) | ||
C、(
| ||
D、[
|
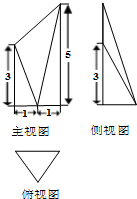 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为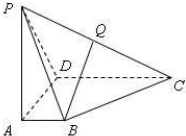 如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=