题目内容
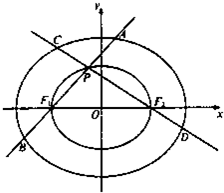 已知椭圆C1:
已知椭圆C1:| x2 |
| 8 |
| y2 |
| 4 |
(1)P为椭圆C1上异于F1,F2的任意一点.设直线PF1的斜率为k1,直线PF2的斜率为k2.求证:k1•k2为定值;
(2)若直线PF1交C2于A,B两点,直线PF2交C2于C,D两点,求|AB|+|CD|的值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)先求出椭圆C2的方程,再求出直线PF1、PF2的斜率,利用P为椭圆C1:
+
=1上的点,化简即可得出结论.
(Ⅱ)直线PF1的方程是y=k1(x+2
),代入椭圆方程并整理,利用韦达定理求得弦长,化简,即可得到结论.
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅱ)直线PF1的方程是y=k1(x+2
| 2 |
解答:
(1)证明:椭圆C1:
+
=1的左、右顶点为(±2
,0),离心率为
,
椭圆C2中c=2
,离心率
=
,∴a=4,∴b=2
,
∴椭圆C2的方程为
+
=1;
设P(x0,y0),则
+
=1,
∴x02-8=-2y02.
∴k1•k2=
•
=
=-
;
(2)解:设A(x1,y1),B(x2,y2),直线PF1的方程是y=k1(x+2
),
代入椭圆方程并整理得(1+2k12)x2+8
k12x+16k12-16=0.
∴x1+x2=-
,x1x2=
∴|AB|=
•|x1-x2|=8-
①,
同理可得|CD|=8-
•
②
∵k1•k2=-
,
∴|CD|=8-
③,
由①③可得|AB|+|CD|=8+8-4=12.
| x2 |
| 8 |
| y2 |
| 4 |
| 2 |
| ||
| 2 |
椭圆C2中c=2
| 2 |
| c |
| a |
| ||
| 2 |
| 2 |
∴椭圆C2的方程为
| x2 |
| 16 |
| y2 |
| 8 |
设P(x0,y0),则
| x02 |
| 8 |
| y02 |
| 4 |
∴x02-8=-2y02.
∴k1•k2=
| y0 | ||
x0+2
|
| y0 | ||
x0-2
|
| y02 |
| x02-8 |
| 1 |
| 2 |
(2)解:设A(x1,y1),B(x2,y2),直线PF1的方程是y=k1(x+2
| 2 |
代入椭圆方程并整理得(1+2k12)x2+8
| 2 |
∴x1+x2=-
8
| ||
| 1+2k12 |
| 16k12-16 |
| 1+2k12 |
∴|AB|=
| 1+k12 |
| 8k12 |
| 1+2k12 |
同理可得|CD|=8-
| ||
| 2 |
8
| ||
| 1+2k22 |
∵k1•k2=-
| 1 |
| 2 |
∴|CD|=8-
| 4 |
| 1+2k12 |
由①③可得|AB|+|CD|=8+8-4=12.
点评:本题考查椭圆的几何性质,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
设集合U={x∈N*|x≤4},A={1,2},B={2,4},则(∁UA)∪B=( )
| A、{1,2} |
| B、{1,2,3,4} |
| C、{3,4} |
| D、{2,3,4} |
 如图示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于C,若|BC|=2|BF|,且|AC|=5,求此抛物线的方程.
如图示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于C,若|BC|=2|BF|,且|AC|=5,求此抛物线的方程. 已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.
已知抛物线C:y=x2.过点M(1,2)的直线l交C于A,B两点.抛物线C在点A处的切线与在点B处的切线交于点P.