题目内容
 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈(
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈(| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
(1)若x1=
| 3 |
| 5 |
(2)过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=
| 4 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:三角函数的求值
分析:(1)由A点的横坐标,结合OA在第一象限求得A点的纵坐标,从而得到sinα=
,cosα=
,代入两角和的余弦公式求得x2;
(2)直接写出△AOC的面积S1,结合(α+
)的正弦值为正值,余弦值为负值写出△BOD的面积S2,再由S1=
S2列式求解tanα的值.
| 4 |
| 5 |
| 3 |
| 5 |
(2)直接写出△AOC的面积S1,结合(α+
| π |
| 4 |
| 4 |
| 3 |
解答:
解:(1)∵x1=
,y1>0,
∴y1=
=
=
,
∴sinα=
,cosα=
.
则x2=cos(α+
)=cosαcos
-sinαsin
=
×
-
×
=-
;
(2)S1=
sinαcosα=
sin2α.
∵α∈(
,
),
∴α+
∈(
,
),
∴S2=-
sin(α+
)cos(α+
)=-
sin(2α+
)=-
cos2α.
∵S1=
S2,
∴sin2α=-
cos2α,即tan2α=-
.
∴
=-
,解得:tanα=2或tanα=-
.
∵α∈(
,
),
∴tanα=2.
| 3 |
| 5 |
∴y1=
| 1-x12 |
1-(
|
| 4 |
| 5 |
∴sinα=
| 4 |
| 5 |
| 3 |
| 5 |
则x2=cos(α+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
| ||
| 10 |
(2)S1=
| 1 |
| 2 |
| 1 |
| 4 |
∵α∈(
| π |
| 4 |
| π |
| 2 |
∴α+
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
∴S2=-
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 4 |
∵S1=
| 4 |
| 3 |
∴sin2α=-
| 4 |
| 3 |
| 4 |
| 3 |
∴
| 2tanα |
| 1-tan2α |
| 4 |
| 3 |
| 1 |
| 2 |
∵α∈(
| π |
| 4 |
| π |
| 2 |
∴tanα=2.
点评:本题考查直线与圆的综合,考查了三角函数的化简求值,解答的关键是理解并熟练运用三角函数线,是中档题.

练习册系列答案
相关题目
 为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了了解某校今年高三男生的身体状况,随机抽查了部分男生,将测得的他们的体重(单位:千克)数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.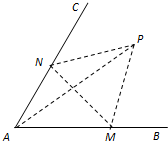 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).