题目内容
已知i为虚数单位,复数
-i的共轭复数的虚部为 .
| 2 |
| 1+i |
考点:复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:利用两个复数代数形式的乘除法法则、虚数单位i的幂运算性质化简复数,求得它的共轭复数,从而得出结论.
解答:
解:∵复数
-i=
-i=1-i-i=1-2i,∴
=1+2i,
故答案为:2.
| 2 |
| 1+i |
| 2(1-i) |
| (1+i)(1-i) |
. |
| z |
故答案为:2.
点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
相关题目
在平面直角坐标平面上,
=(1,4),
=(-3,1),且
与
在直线l的方向向量上的投影的长度相等,则直线l的斜率为( )
| OA |
| OB |
| OA |
| OB |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
若复数z满足z•(1-i)=2-i(其中i是虚数单位),则z=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若直线y=|
|x+1与直线y=|
|x平行,
,
为非零向量,则必有( )
| a |
| b |
| a |
| b |
A、
| ||||||||
B、
| ||||||||
C、(
| ||||||||
D、(
|
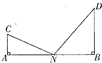 如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为
如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为