题目内容
在△ABC中,己知
•
=9,sinB=sinCcosA,又△ABC的面积为6
(1)求△ABC的三边长;
(2)若D为BC边上的一点,且CD=1,求tan∠BAD.
| AB |
| AC |
(1)求△ABC的三边长;
(2)若D为BC边上的一点,且CD=1,求tan∠BAD.
考点:平面向量数量积的运算,两角和与差的正切函数
专题:平面向量及应用
分析:(1)利用两角和的正弦公式、数量积运算和三角形的面积公式、勾股定理即可得出;
(2)由两角和差的正切公式即可得出.
(2)由两角和差的正切公式即可得出.
解答:
解(1)设三边分别为a,b,c.
∵sinB=sinCcosA,
∴sin(A+C)=sinCcosA,
化为sinAcosC+cosAsinC=sinCcosA,
∴sinAcosC=0,
∴cosC=0,∴C=
.
又
两式相除可得tanA=
=
令a=4k,b=3k(k>0),
∴S=
ab=6,∴
×4k×3k=6,解得k=1.
∴三边长分别为3,4,5,
(2)由(1)可得:tan∠BAC=
,tan∠DAC=
,
∴tan∠BAD=tan(∠BAC-∠DAC)=
=
=
.
∵sinB=sinCcosA,
∴sin(A+C)=sinCcosA,
化为sinAcosC+cosAsinC=sinCcosA,

∴sinAcosC=0,
∴cosC=0,∴C=
| π |
| 2 |
又
|
两式相除可得tanA=
| 4 |
| 3 |
| a |
| b |
令a=4k,b=3k(k>0),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴三边长分别为3,4,5,
(2)由(1)可得:tan∠BAC=
| 4 |
| 3 |
| 1 |
| 3 |
∴tan∠BAD=tan(∠BAC-∠DAC)=
| tan∠BAC-tan∠DAC |
| 1+tan∠BACtan∠DAC |
| ||||
1+
|
| 9 |
| 13 |
点评:本题考查了两角和的正弦公式、数量积运算和三角形的面积公式、勾股定理、两角和差的正切公式等基础知识与基本技能方法,考查了计算能力,属于难题.

练习册系列答案
相关题目
一批货物随17列货车从A市以v千米/小时匀速直达B市,已知两地铁路线长为400千米,为了安全,两列货车的间距不得少于(
)2千米,那么这批货物全部运到B市最快需要( )
| v |
| 20 |
| A、6小时 | B、8小时 |
| C、10小时 | D、12小时 |
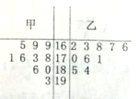 甲、乙两名工人生产的零件尺寸记成如图所示的茎叶图,已知零件尺寸在区间[165,180]内的为合格品.(单位:mm)
甲、乙两名工人生产的零件尺寸记成如图所示的茎叶图,已知零件尺寸在区间[165,180]内的为合格品.(单位:mm)