Question

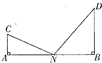如图，C、D是两个小区所在地，C、D到一条公路AB的垂直距离分别为CA=1km，DB=2km，A、B间的距离为3km，某公交公司要在A、B之间的某点N处建造一个公交站点，使得N对C、D两个小区的视角∠CND最大，则N处与A处的距离为

 

km．

Answer 1

考点：解三角形的实际应用

专题：应用题,三角函数的求值

分析：设出NA的长度x，把∠CNA与∠DNB的正切值用含有x的代数式表示，最后把∠CND的正切值用含有x的代数式表示，换元后再利用基本不等式求最值，最后得到使N对C、D两个小区的视角∠CND最大时的x值，即可确定点N的位置．

解答： 解：设NA=x，∠CNA=α，∠DNB=β．
依题意有tanα=

1

x

，tanβ=

2

3-x

，
tan∠CND=tan[π-（α+β）]=-tan（α+β）=-

1 x + 2 3-x

1- 1 x • 2 3-x

=

x+3

x2-3x+2

，
令t=x+3，由0＜x＜3，得3＜t＜6，
则tan∠CND=

t

t2-9t+20

=

1

t+ 20 t -9

∵4

5

≤t+

20

t

＜3+

20

3

∴t=2

5

，即x=2

5

-3时取得最大角，
故N处与A处的距离为（2

5

-3）km．
故答案为：2

5

-3．

点评：本题考查解三角形的实际应用，考查了利用基本不等式求最值，解答的关键是把实际问题转化为数学问题，是中档题．