题目内容
4.已知三棱锥P-ABC的所有顶点都在半径为1的球O的球面上,△ABC是边长为1的正三角形,PC为球O的直径,则该三棱锥的底面ABC上的高为( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
分析 根据题意,利用截面圆的性质即可求出点O到平面ABC的距离,进而求出点P到平面ABC的距离.
解答 解:因为△ABC是边长为1的正三角形,所以△ABC外接圆的半径r=$\frac{\sqrt{3}}{3}$,
所以点O到平面ABC的距离d=$\frac{\sqrt{6}}{3}$,
PC为球O的直径,点P到平面ABC的距离为2d=$\frac{2\sqrt{6}}{3}$,
故选:D.
点评 本题考查三棱锥的底面ABC上的高,考查学生的计算能力,求出点O到平面ABC的距离,进而求出点P到平面ABC的距离是关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
13.在正四棱锥P-ABCD中,PA=2,E为PC的中点,若异面直线PA与BE所成角为45°,则四棱锥P-ABCD的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
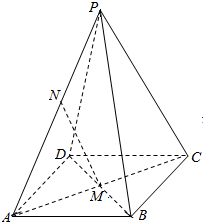 (理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.
(理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.