题目内容
16.(普通班)设动点P(x,y)到定点F($\frac{1}{2}$,0)的距离比到y轴的距离大$\frac{1}{2}$.记点P的轨迹为曲线C.(1)求点P的轨迹方程;
(2)过F($\frac{1}{2}$,0)作直线m交曲线C(x≥0)于A、B两点,若以AB为直径的圆过点D(0,$\frac{1}{2}$),求三角形ABD的面积.
分析 (1)设出动点P的坐标,分P的横坐标小于等于0和大于0两种情况讨论,横坐标小于等于0时明显看出P的轨迹是x轴负半轴,x大于0时直接由题意列式化简整理即可..
(2)设直线m的方程为x=my+$\frac{1}{2}$,A(x1,y1),B(x2,y2),x=my+$\frac{1}{2}$代入y2=2x,可得y2-2my-1=0,分类讨论,结合以AB为直径的圆过点D(0,$\frac{1}{2}$),求出m,即可求三角形ABD的面积.
解答 解:(1)P到定点F($\frac{1}{2}$,0)的距离为$\sqrt{(x-\frac{1}{2})^{2}+{y}^{2}}$,P到y轴的距离为|x|,
∴动点P到定点定点F($\frac{1}{2}$,0)的距离比到y轴的距离大$\frac{1}{2}$,
∴列出等式:$\sqrt{(x-\frac{1}{2})^{2}+{y}^{2}}$-|x|=1
当x≤0时,P的轨迹为y=0(x≤0);
当x>0时,又化简得y2=2x为焦点为F($\frac{1}{2}$,0)的抛物线.
则动点P的轨迹方程为:y2=$\left\{\begin{array}{l}{2x,x>0}\\{0,x≤0}\end{array}\right.$;
(2)设直线m的方程为x=my+$\frac{1}{2}$,A(x1,y1),B(x2,y2),
x=my+$\frac{1}{2}$代入y2=2x,可得y2-2my-1=0
∴y1y2=-1,x1x2=(my1+$\frac{1}{2}$)(my2+$\frac{1}{2}$)=-2m2+$\frac{1}{4}$,
∴以AB为直径的圆过D(0,$\frac{1}{2}$),
∴(-x1,$\frac{1}{2}$-y1)•(-x2,$\frac{1}{2}$-y2)=0,
∴x1x2+($\frac{1}{2}$-y1)•($\frac{1}{2}$-y2)=0,
∴x1x2+y1y2+$\frac{1}{4}$-$\frac{1}{2}$(y1+y2)=0,
∴-2m2+$\frac{1}{4}$-1+$\frac{1}{4}$-$\frac{1}{2}$×2m=0,解得m=0或-$\frac{1}{2}$,
m=0时,直线m的方程为x=$\frac{1}{2}$,|AB|=2,三角形ABD的面积S=$\frac{1}{2}×2×\frac{1}{2}$=$\frac{1}{2}$;
m=-$\frac{1}{2}$时,直线m的方程为x=-$\frac{1}{2}$y+$\frac{1}{2}$,|AB|=$\frac{\sqrt{5}}{2}$,d=$\frac{\frac{1}{4}}{\sqrt{1+\frac{1}{4}}}$=$\frac{\sqrt{5}}{10}$三角形ABD的面积S=$\frac{1}{2}×\frac{\sqrt{5}}{2}$×$\frac{\sqrt{5}}{10}$=$\frac{1}{8}$.
点评 本题考查了抛物线的方程,考查了分类讨论的数学思想方法,是中档题.

| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
| A. | $\frac{5}{6}$ | B. | $\frac{11}{12}$ | C. | $\frac{10}{11}$ | D. | $\frac{5}{12}$ |
| A. | 2-$\frac{1}{{2}^{n}}$ | B. | 1-$\frac{1}{{2}^{n}}$ | C. | 1-$\frac{1}{{2}^{n+1}}$ | D. | $\frac{1}{{2}^{n}}$ |
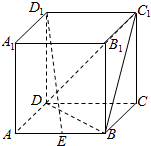 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.