题目内容
14.已知曲线C1的参数方程为$\left\{\begin{array}{l}x=3+4coxθ\\ y=4+4sinθ\end{array}\right.$(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4sinθ.(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点所在直线的极坐标方程.
分析 (1)由$\left\{\begin{array}{l}x=3+4coxθ\\ y=4+4sinθ\end{array}\right.$消去θ,得C1的直角坐标方程,再将x=ρcosφ,y=ρsinφ代入能求出C1的极坐标方程.
(2)先求出C2的直角坐标方程,和C1的直角坐标方程联立,求出C1、C2的交点所在直线方程,由此能求出其极坐标方程.
解答 (1)解:∵曲线C1的参数方程为$\left\{\begin{array}{l}x=3+4coxθ\\ y=4+4sinθ\end{array}\right.$(θ为参数),
∴由$\left\{\begin{array}{l}x=3+4coxθ\\ y=4+4sinθ\end{array}\right.$消去θ,得C1的直角坐标方程:(x-3)2+(y-4)2=16,(2分)
即x2+y2-6x-8y+9=0
将x=ρcosφ,y=ρsinφ代入得C1的极坐标方程为ρ2-6ρcosφ-8ρsinφ+9=0.(4分)
(2)解:∵曲线C2的极坐标方程为ρ=4sinθ,
由ρ=4sinθ,得C2的普通方程为:x2+y2-4y=0,(6分)
由$\left\{\begin{array}{l}{x^2}+{y^2}-6x-8y+9=0\\{x^2}+{y^2}-4y=0\end{array}\right.$,得:6x+4y-9=0,(8分)
∴C1、C2的交点所在直线方程为6x+4y-9=0
∴其极坐标方程为:6ρcosθ+4ρsinθ-9=0.(10分)
点评 本题考查极坐标方程的求法,是基础题,解题时要认真审题,注意直角坐标、极坐标互化公式的合理运用.

练习册系列答案
相关题目
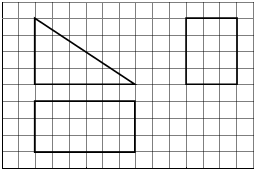
4.如图,网格纸的各小格都是正方形,粗实线画出的是一个凸多面体的三视图(两个矩形,一个直角三角形),则这个几何体可能为( )

| A. | 三棱台 | B. | 三棱柱 | C. | 四棱柱 | D. | 四棱锥 |
5.已知sinφ=$\frac{3}{5}$,且φ∈($\frac{π}{2}$,π),函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于$\frac{π}{2}$,则f($\frac{π}{4}$)的值为( )
| A. | -$\frac{3}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.已知三棱锥P-ABC的所有顶点都在半径为1的球O的球面上,△ABC是边长为1的正三角形,PC为球O的直径,则该三棱锥的底面ABC上的高为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
