题目内容
12.已知直线l过点P(0,-2),且与以A(1,-1)B(2,-4)为端点的线段AB总有公共点,求直线l倾斜角的取值范围[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π).分析 先求出直线的斜率的取值范围,再根据斜率与倾斜角的关系以及倾斜角的范围求出倾斜角的具体范围.
解答 解:设直线l的斜率等于k,
由题意知,k≥kPB且k≤KPA,即k≥$\frac{-4+2}{2-0}$=-1,且k≤$\frac{-1+2}{1-0}$=1,
即-1≤k≤1,
设直线的倾斜角为α,则α∈[0,π),tanα=k,
∴-1≤tanα≤1,
∴0≤α≤$\frac{π}{4}$,或$\frac{3π}{4}$≤α<π,
故答案为:[0,$\frac{π}{4}$]∪[$\frac{3π}{4}$,π).
点评 本题考查直线的倾斜角和斜率的关系,直线的斜率公式的应用,属于基础题.

练习册系列答案
相关题目
17.已知抛物线x2=8y的焦点为F,在抛物线内有一点A(4,4),若该抛物线上存在一动点P,则|PA|+|PF|的最小值为( )
| A. | $4\sqrt{2}+2$ | B. | 4 | C. | $2\sqrt{5}$ | D. | 6 |
4.已知三棱锥P-ABC的所有顶点都在半径为1的球O的球面上,△ABC是边长为1的正三角形,PC为球O的直径,则该三棱锥的底面ABC上的高为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
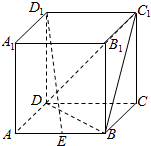 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.