题目内容
15.下列说法正确的是( )| A. | 异面直线所成的角范围是[0,π] | |
| B. | 命题“?x∈R,2x>0”的否定是“?x∈R,2x>0” | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | x2>1成立的一个充分而不必要的条件是x>2 |
分析 根据异面直线所成的角范围,可判断A;写出原命题的否定,可判断B;根据复合命题真假判断的真值表,可判断C;根据充要条件的定义,可判断D.
解答 解:选项A,异面直线所成的角范围是$({0,\frac{π}{2}}]$,故错误;
选项B,命题“?x∈R,2x>0”的否定应该是?x∈R,2x≤0,故错误;
选项C,若p∧q为假命题,则只要p,q中有一个为假即可,故错误;
选项D,x2>1成立的一个充分而不必要的条件是x>2,可以判定成立.
故选:D
点评 本题以命题的真假判断与应用为载体,考查了命题的否定,复合命题,充要条件,异面直线所成的角等知识点,难度基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
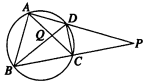 如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )
如图所示,圆内接四边形ABCD的一组对边AD,BC的延长线相交于点P,对角线AC,BD相交于点Q,则图中相似三角形共有( )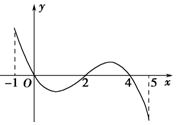 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题: