如图所示.圆内接四边形ABCD的一组对边AD.BC的延长线相交于点P.对角线AC.BD相交于点Q.则图中相似三角形共有( )A．4对B．2对C．5对D．3对题目和参考答案——青夏教育精英家教网—

题目内容

20．

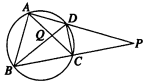如图所示，圆内接四边形ABCD的一组对边AD，BC的延长线相交于点P，对角线AC，BD相交于点Q，则图中相似三角形共有（　　）

A．

4对

B．

2对

C．

5对

D．

3对

分析根据圆周角定理，圆内接四边形的性质等知识，找出图中的相等角，然后根据相等角去找相似三角形．

解答解：∵∠DAQ=∠CBQ，∠BCQ=∠ADQ，
∴△DAQ∽△CBQ，同理可得：△DCQ∽△ABQ，
∵四边形ABCD是⊙O的内接四边形，
∴∠PDC=∠PBA，∠PCD=∠PAB，
∴△PCD∽△PAB，
∵∠DPB=∠CPA（公共角），∠PBD=∠PAC（同弧所对的圆周角相等），
∴△PBD∽△PAC．
因此本题共有4对相似三角形，
故选A．

点评本题考查圆周角定理、相似三角形的判定、圆内接四边形等知识的应用能力．

练习册系列答案

暑假自主学习手册江苏人民出版社系列答案

暑假生活江西高校出版社系列答案

暑假作业贵州人民出版社系列答案

暑假作业教育科学出版社系列答案

新课标暑假作业二十一世纪出版社系列答案

相关题目

10．

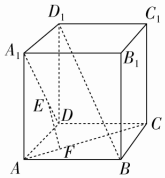如图所示，在正方体ABCD-A₁B₁C₁D₁中，E、F分别在A₁D、AC上，且A₁E=$\frac{2}{3}$A₁D，AF=$\frac{1}{3}$AC，则（　　）

	A．	EF至多与A₁D、AC之一垂直		B．	EF与A₁D、AC都垂直
	C．	EF与BD₁相交		D．	EF与BD₁异面

11．复数z=$\frac{1+i}{i}$，$\overline z$是它的共轭复数，则$z•\overline z$=2．

8．已知x，y满足$\left\{\begin{array}{l}x+2y-3≤0\\ x+3y-3≥0\\ y≤1\end{array}\right.$，z=2x+y的最大值是m，若正数a，b满足a+b=m，则$\frac{1}{a}+\frac{4}{b}$的最小值为$\frac{3}{2}$．

15．下列说法正确的是（　　）

	A．	异面直线所成的角范围是[0，π]
	B．	命题“?x∈R，2^x＞0”的否定是“?x∈R，2^x＞0”
	C．	若p∧q为假命题，则p，q均为假命题
	D．	x²＞1成立的一个充分而不必要的条件是x＞2

5．下列函数中，在（-∞，0）内为减函数的是（　　）

12．若对任意x∈[2，4]及y∈[2，3]，该不等式xy≤ax²+2y²恒成立，则实数a的范围是a≥0．

9．已知全集U=R，集合A={x|x²-2x-3＞0}，B={x|4-x²≤0}，求：
（1）A∩B；
（2）（∁_UA）∪（∁_UB）．

10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右交点分别为F₁，F₂，且|F₁F₂|=4$\sqrt{3}$，A（$\sqrt{3}$，-$\frac{\sqrt{13}}{2}$）是椭圆上一点．
（1）求椭圆C的标准方程和离心率e的值；
（2）若T为椭圆C上异于顶点的任意一点，M，N分别为椭圆的右顶点和上顶点，直线TM与y轴交于点P，直线TN与x轴交于点Q，求证：|PN|•|QM|为定值．

试题分类