题目内容
5.与函数f(x)=2x的图象关于直线y=x对称的曲线C对应的函数为g(x),则函数$y=g({\frac{1}{x}})•g({4x})({\frac{1}{8}≤x≤4})$的值域为[-8,1].分析 根据题意写出函数g(x),求出函数y的解析式,再根据x的取值范围求出y的最大、最小值即可.
解答 解:∵函数f(x)=2x,
∴g(x)=log2x,x>0;
∴函数y=g($\frac{1}{x}$)•g(4x)
=log2$\frac{1}{x}$•log2(4x)
=(-log2x)•(2+log2x)
=-2log2x-${{log}_{2}}^{2}$x
=-${{(log}_{2}x+1)}^{2}$+1;
又$\frac{1}{8}$≤x≤4,
∴-3≤log2x≤2,
当x=$\frac{1}{2}$时,log2$\frac{1}{2}$=-1,y取得最大值为ymax=1;
当x=4时,log24=2,y取得最小值为ymin=-8;
∴y的值域为[-8,1].
故答案为:[-8,1].
点评 本题考查了反函数与复合函数的值域问题,也考查了对数函数与二次函数的最值问题,是基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.已知α∈R,则“cosα=-$\frac{\sqrt{3}}{2}$”是“α=2kπ+$\frac{5π}{6}$,k∈Z”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
20.设α为△ABC的内角,且tanα=-$\frac{3}{4}$,则cos2α的值为( )
| A. | $\frac{7}{25}$ | B. | -$\frac{24}{25}$ | C. | -$\frac{1}{25}$ | D. | $\frac{1}{25}$ |
10.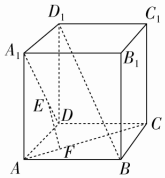 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=$\frac{2}{3}$A1D,AF=$\frac{1}{3}$AC,则( )| A. | EF至多与A1D、AC之一垂直 | B. | EF与A1D、AC都垂直 | ||
| C. | EF与BD1相交 | D. | EF与BD1异面 |
15.下列说法正确的是( )
| A. | 异面直线所成的角范围是[0,π] | |
| B. | 命题“?x∈R,2x>0”的否定是“?x∈R,2x>0” | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | x2>1成立的一个充分而不必要的条件是x>2 |