题目内容
13.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,x)且$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,则|3$\overrightarrow{b}$|的值为( )| A. | $\sqrt{140}$ | B. | $\frac{3}{2}\sqrt{85}$ | C. | $\sqrt{120}$ | D. | $\sqrt{110}$ |
分析 由已知求出$\overrightarrow{a}$-2$\overrightarrow{b}$的坐标,结合数量积为0求得x,再由模的公式求解.
解答 解:∵$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,x),
∴$\overrightarrow{a}$-2$\overrightarrow{b}$=(-4,1-2x),
由$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,得2×(-4)+1×(1-2x)=-8+1-2x=0,
即x=-$\frac{7}{2}$.
∴$\overrightarrow{b}=(3,-\frac{7}{2})$,则|$3\overrightarrow{b}$|=3×$\sqrt{9+\frac{49}{4}}$=$\frac{3}{2}\sqrt{85}$.
故选:B.
点评 本题考查平面向量的数量积运算,考查了向量垂直的坐标运算,是基础题.

练习册系列答案
相关题目
5.设函数f(x)=cosx+2sinx,则f′($\frac{π}{4}$)=( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\sqrt{2}$ |
18.某四棱锥的三视图如图所示,该四棱锥的表面积为( )


| A. | $1+\sqrt{2}$ | B. | 3 | C. | $2+\sqrt{2}$ | D. | 4 |
2.如图,已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD一定是( )
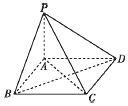

| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 非上述三种图形 |
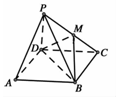 已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上
已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上