题目内容
1.已知动点M(x,y)到定点F(0,2)的距离等于M到x轴的距离,求证:点M的轨迹方程是y=$\frac{{x}^{2}}{4}$+1.分析 由题意,$\sqrt{{x}^{2}+(y-2)^{2}}$=|y|,化简可得点M的轨迹方程
解答 证明:由题意,$\sqrt{{x}^{2}+(y-2)^{2}}$=|y|,化简可得点M的轨迹方程是y=$\frac{{x}^{2}}{4}$+1.
点评 本题考查了与直线有关的动点的轨迹方程,考查了两点间的距离公式,是中档题.

练习册系列答案
相关题目
13.已知直线3x-2y=0与圆(x-m)2+y2=1相交,则正整数m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.执行如图所示的程序框图,则输出的结果为( )


| A. | 10 | B. | 17 | C. | 24 | D. | 26 |
13.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,x)且$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,则|3$\overrightarrow{b}$|的值为( )
| A. | $\sqrt{140}$ | B. | $\frac{3}{2}\sqrt{85}$ | C. | $\sqrt{120}$ | D. | $\sqrt{110}$ |
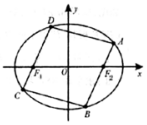 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的周长为6
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴的一个顶点与两个焦点构成正三角形,且该三角形的周长为6