题目内容
4.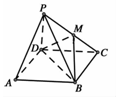 已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上
已知四棱锥P-ABCD的底面为平行四边形,PD⊥平面ABCD,M在边PC上(Ⅰ)当M在边PC上什么位置时,AP∥平面MBD?并给出证明.
(Ⅱ)在(Ⅰ)条件之下,若AD⊥PB,求证:BD⊥平面PAD.
分析 (Ⅰ)M是PC中点时,AC与BD的交点O是AC的中点,从而OM∥PA,由此能证明AP∥平面MBD.
(Ⅱ)推导出PD⊥AD,AD⊥BD,PD⊥BD,由此能证明BD⊥平面PAD.
解答 解:(Ⅰ)M是PC中点时,AP∥平面MBD.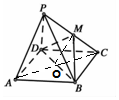
证明:∵底面ABCD是平行四边形,
∴AC与BD的交点O是AC的中点,
又M是PC的中点,∴OM∥PA,
∵OM?平面MBD,AP?平面MBD,
∴AP∥平面MBD.
证明:(Ⅱ)∵PD⊥平面ABCD,AD?平面ABCD,∴PD⊥AD,
又AD⊥PB,PD∩PB=P,∴AD⊥平面PBD,∴AD⊥BD,
∵PD⊥平面ABCD,BD?平面ABCD,
∴PD⊥BD,
∵PD∩AD=D,∴BD⊥平面PAD.
点评 本题考查满足线面平行的点的位置的确定与证明,考查线面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
19.已知双曲线以△ABC的顶点B,C为焦点,且经过点A,若△ABC内角的对边分别为a,b,c.且a=4,b=5,$c=\sqrt{21}$,则此双曲线的离心率为( )
| A. | $5-\sqrt{21}$ | B. | $\frac{{\sqrt{21}+5}}{2}$ | C. | $5+\sqrt{21}$ | D. | $\frac{{5-\sqrt{21}}}{2}$ |
9.在等差数列{an}中,a2=3,a3+a6=11
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+$\frac{1}{{2}^{{a}_{n}}}$,其中n∈N*,求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=an+$\frac{1}{{2}^{{a}_{n}}}$,其中n∈N*,求数列{bn}的前n项和Sn.
13.已知直线3x-2y=0与圆(x-m)2+y2=1相交,则正整数m的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,x)且$\overrightarrow{a}$•($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,则|3$\overrightarrow{b}$|的值为( )
| A. | $\sqrt{140}$ | B. | $\frac{3}{2}\sqrt{85}$ | C. | $\sqrt{120}$ | D. | $\sqrt{110}$ |