题目内容
已知抛物线x2=2py(p>0)的焦点为F,点A为抛物线上的一点,其纵坐标为1,|AF|=
.
(Ⅰ)求抛物线的方程;
(Ⅱ)设B,C为抛物线上不同于A的两点,且AB⊥AC,过B,C两点分别作抛物线的切线,记两切线的交点为D,求|OD|的最小值.
| 5 |
| 4 |
(Ⅰ)求抛物线的方程;
(Ⅱ)设B,C为抛物线上不同于A的两点,且AB⊥AC,过B,C两点分别作抛物线的切线,记两切线的交点为D,求|OD|的最小值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由点A为抛物线上的一点,其纵坐标为1,|AF|=
,根据抛物线的定义,即可求抛物线的方程;
(Ⅱ)求出B、C处的切线方程,联立求出D的坐标,结合A(1,1)且AB⊥AC,求出|OD|,即可求出|OD|的最小值.
| 5 |
| 4 |
(Ⅱ)求出B、C处的切线方程,联立求出D的坐标,结合A(1,1)且AB⊥AC,求出|OD|,即可求出|OD|的最小值.
解答:
解:(Ⅰ)由抛物线定义得:|AF|=yA+
,
∴
+1=
,
∴p=
------(2分)
∴抛物线方程为x2=y------(4分)
(Ⅱ)设B(x1,
),C(x2,
),则
∵A(1,1)且AB⊥AC,
∴
•
=-1
即(x1+x2)+x1•x2=-2------(6分)
又∵y′=2x,∴B、C处的切线的斜率为k1=2x1,k2=2x2,
∴B、C处的切线方程为y-
=2x1(x-x1)和y-
=2x2(x-x2)
由
得D(
,x1x2)------(8分)
设x1x2=t,由(x1+x2)+x1•x2=-2得
=-1-
,
∴|OD|2=(-1-
)2+t2=
t2+t+1------(10分)
当t=-
时,|OD|2min=
,
∴|OD|min=
------(12分)
| p |
| 2 |
∴
| p |
| 2 |
| 5 |
| 4 |
∴p=
| 1 |
| 2 |
∴抛物线方程为x2=y------(4分)
(Ⅱ)设B(x1,
| x | 2 1 |
| x | 2 2 |
∵A(1,1)且AB⊥AC,
∴
| ||
|
| ||
|
即(x1+x2)+x1•x2=-2------(6分)
又∵y′=2x,∴B、C处的切线的斜率为k1=2x1,k2=2x2,
∴B、C处的切线方程为y-
| x | 2 1 |
| x | 2 2 |
由
|
| x1+x2 |
| 2 |
设x1x2=t,由(x1+x2)+x1•x2=-2得
| x1+x2 |
| 2 |
| t |
| 2 |
∴|OD|2=(-1-
| t |
| 2 |
| 5 |
| 4 |
当t=-
| 2 |
| 5 |
| 4 |
| 5 |
∴|OD|min=
2
| ||
| 5 |
点评:本题考查抛物线的定义与方程,考查抛物线的切线方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知变量x,y满足约束条件
,则z=x+2y的最大值为( )
|
| A、6 | B、5 | C、4 | D、3 |
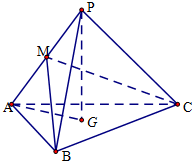 如图,三棱锥P-ABC中,AB=AC=2
如图,三棱锥P-ABC中,AB=AC=2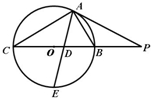 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.