题目内容
函数f(x)=sinx.
(Ⅰ)令f1(x)=f′(x),fn+1(x)=
(x),(n∈N*),求f2014(x)的解析式;
(Ⅱ)若f(x)+1≥ax+cosx在[0,π]上恒成立,求实数a的取值范围;
(Ⅲ)证明:f(
)+f(
)+…+f(
)≥
.
(Ⅰ)令f1(x)=f′(x),fn+1(x)=
| f | ′ n |
(Ⅱ)若f(x)+1≥ax+cosx在[0,π]上恒成立,求实数a的取值范围;
(Ⅲ)证明:f(
| π |
| 2n+1 |
| 2π |
| 2n+1 |
| (n+1)π |
| 2n+1 |
3
| ||
| 4(2n+1) |
考点:数列递推式
专题:导数的综合应用,点列、递归数列与数学归纳法
分析:(Ⅰ)求函数的导数,根据导数之间的关系得到函数的周期性即可求f2014(x)的解析式;
(Ⅱ)法1:将不等式f(x)+1≥ax+cosx在[0,π]上恒成立,进行参数分离,即可求实数a的取值范围;
法2;构造函数,利用导数研究函数的单调性,也可求a的取值范围.
(Ⅲ)根据(Ⅱ)的结论即可证明不等式.
(Ⅱ)法1:将不等式f(x)+1≥ax+cosx在[0,π]上恒成立,进行参数分离,即可求实数a的取值范围;
法2;构造函数,利用导数研究函数的单调性,也可求a的取值范围.
(Ⅲ)根据(Ⅱ)的结论即可证明不等式.
解答:
解:(Ⅰ)f1(x)=cosx,f2(x)=-sinx,f3(x)=-cosx,f4(x)=sinx…周期为4,
∴f2014(x)=f503×4+2(x)=f2(x)=-sinx.
(Ⅱ)方法一:即sinx+1≥ax+cosx在[0,π]上恒成立,
当x=0时,a∈R;
当x∈(0,π]时,a≤
,
设g(x)=
,g′(x)=
=
,
设h(x)=xcosx+xsinx-sinx+cosx-1,h′(x)=x(cosx-sinx),
则x∈(0,
)时h′(x)>0,h(x)增;x∈(
,π],h(x)减.
而h(0)=0,h(
)>0,h(π)<0,
∴h(x)在(
,π]上存在唯一零点,
设为x0,则x∈(0,x0),h(x)>0,g(x)>0;x∈(x0,π],h(x)<0,g(x)<0,
∴g(x)在x0处取得最大值,在x=π处取得最小值,∴a≤g(π)=
.
综上:∴a≤
.
方法二:设g(x)=sinx+1-ax-cosx,g′(x)=cosx-a+sinx=
sin(x+
)-a.
∵x∈[0,π],∴
sin(x+
)∈[-1,
].
当a≤-1时,g′(x)≥0在[0,π]上恒成立,
∴g(x)≥g(x)min=g(0)=0成立,故a≤-1;
当a≥
时,g′(x)≤0在[0,π]上恒成立,g(x)min=g(π)=2-πa≥0得a≤
,无解.
当-1<a<
时,则存在x0∈(0,π]使得x∈(0,x0)时g(x)增,x∈(x0,π]时g(x)减,
故g(x)min={g(0),g(π)},
∴
,解得a≤
,故-1<a≤
.
综上:∴a≤
.
(Ⅲ)由(Ⅱ)知:x∈[0,π]时sinx+1≥
x+cosx,
∴sinx-cosx≥
x-1
即
sin(x-
)≥
x-1.
当1≤k≤n+1时,0≤
+
≤π,
∴
sin
=
sin(
+
-
)≥
(
+
)-1=
-
,
∴
[f(
)+f(
+…+f(
)]≥(
-
)+…+(
-
=
•
-
=
,
∴f(
)+f(
)+…+f(
)≥
.
∴f2014(x)=f503×4+2(x)=f2(x)=-sinx.
(Ⅱ)方法一:即sinx+1≥ax+cosx在[0,π]上恒成立,
当x=0时,a∈R;
当x∈(0,π]时,a≤
| sinx-cosx+1 |
| x |
设g(x)=
| sinx-cosx+1 |
| x |
| (cosx+sinx)x-(sinx-cos+1) |
| x2 |
| xcosx+xsinx-sinx+cosx-1 |
| x2 |
设h(x)=xcosx+xsinx-sinx+cosx-1,h′(x)=x(cosx-sinx),
则x∈(0,
| π |
| 4 |
| π |
| 4 |
而h(0)=0,h(
| π |
| 4 |
∴h(x)在(
| π |
| 4 |
设为x0,则x∈(0,x0),h(x)>0,g(x)>0;x∈(x0,π],h(x)<0,g(x)<0,
∴g(x)在x0处取得最大值,在x=π处取得最小值,∴a≤g(π)=
| 2 |
| π |
综上:∴a≤
| 2 |
| π |
方法二:设g(x)=sinx+1-ax-cosx,g′(x)=cosx-a+sinx=
| 2 |
| π |
| 4 |
∵x∈[0,π],∴
| 2 |
| π |
| 4 |
| 2 |
当a≤-1时,g′(x)≥0在[0,π]上恒成立,
∴g(x)≥g(x)min=g(0)=0成立,故a≤-1;
当a≥
| 2 |
| 2 |
| π |
当-1<a<
| 2 |
故g(x)min={g(0),g(π)},
∴
|
| 2 |
| π |
| 2 |
| π |
综上:∴a≤
| 2 |
| π |
(Ⅲ)由(Ⅱ)知:x∈[0,π]时sinx+1≥
| 2 |
| π |
∴sinx-cosx≥
| 2 |
| π |
即
| 2 |
| π |
| 4 |
| 2 |
| π |
当1≤k≤n+1时,0≤
| kπ |
| 2n+1 |
| π |
| 4 |
∴
| 2 |
| kπ |
| 2n+1 |
| 2 |
| kπ |
| 2n+1 |
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| kπ |
| 2n+1 |
| π |
| 4 |
| 2k |
| 2n+1 |
| 1 |
| 2 |
∴
| 2 |
| π |
| 2n+1) |
| 2π |
| 2n+1) |
| (n+1)π |
| 2n+1 |
| 2 |
| 2n+1 |
| 1 |
| 2 |
| 2(n+1) |
| 2n+1 |
| 1 |
| 2 |
=
| 2 |
| 2n+1 |
| (n+1)(n+2) |
| 2 |
| n+1 |
| 2 |
| 3(n+1) |
| 2(2n+1) |
∴f(
| π |
| 2n+1 |
| 2π |
| 2n+1 |
| (n+1)π |
| 2n+1 |
3
| ||
| 4(2n+1) |
点评:本题主要考查数列的递推公式的应用,不等式恒成立以及不等式的证明,涉及的知识点较多,综合性较强,难度较大.

练习册系列答案
相关题目
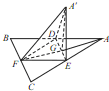 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: