题目内容
有以下四个命题:
①函数f(x)=sin(
-2x)的一个增区间是[
,
];
②函数f(x)=sin(ωx+φ)为奇函数,则φ为π的整数倍;
③对于函数f(x)=tan(2x+
),若f(x1)=f(x2),则x1-x2必是π的整数倍;
④y=|sinx|最小正周期为π;
其中正确的命题是 .(填上正确命题的序号)
①函数f(x)=sin(
| π |
| 3 |
| 5π |
| 12 |
| 11π |
| 12 |
②函数f(x)=sin(ωx+φ)为奇函数,则φ为π的整数倍;
③对于函数f(x)=tan(2x+
| π |
| 3 |
④y=|sinx|最小正周期为π;
其中正确的命题是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:通过求解复合函数的单调区间判断命题①;
由函数的奇偶性的性质,取x=0得f(x)=0,由此求φ的值加以判断;
直接由正切函数的周期性加以判断;
写出分段函数,画出函数图象,由图象求得函数周期.
由函数的奇偶性的性质,取x=0得f(x)=0,由此求φ的值加以判断;
直接由正切函数的周期性加以判断;
写出分段函数,画出函数图象,由图象求得函数周期.
解答:
解:对于①:即求f(x)=sin(2x-
)的减区间,
由2kπ+
≤2x-
≤2kπ+
(k∈Z),得x∈[kπ+
,kπ+
],
∴f(x)=sin(
-2x)的一个增区间是[
,
],
∴①对;
对于②:f(x)=sin(ωx+φ)为奇函数,则f(0)=sin(ω•0+φ)=0,
∴φ=kπ(k∈Z),反之也成立,即②对;
对于③:x1-x2应是周期的整数倍,又周期为T=
,∴③错;
对于④:y=|sinx|=
,图象如图,
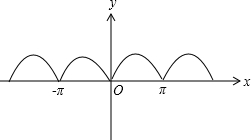
∴y=|sinx|最小正周期为π,∴④对.
∴正确的命题是①②④.
故答案为:①②④.
| π |
| 3 |
由2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
∴f(x)=sin(
| π |
| 3 |
| 5π |
| 12 |
| 11π |
| 12 |
∴①对;
对于②:f(x)=sin(ωx+φ)为奇函数,则f(0)=sin(ω•0+φ)=0,
∴φ=kπ(k∈Z),反之也成立,即②对;
对于③:x1-x2应是周期的整数倍,又周期为T=
| π |
| 2 |
对于④:y=|sinx|=
|

∴y=|sinx|最小正周期为π,∴④对.
∴正确的命题是①②④.
故答案为:①②④.
点评:本题考查命题真假性的判断及应用,考查了与三角函数有关的复合函数的性质,是中档题.

练习册系列答案
相关题目
设i是虚数单位,则复数z=(
)2014=( )
| 1+i |
| 1-i |
| A、-1 | B、1 | C、-i | D、i |
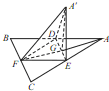 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: