题目内容
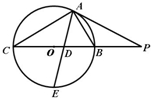如图所示，PA为圆O的切线，A为切点，PO交圆O于B，C两点，PA=20，PB=10，∠BAC的角平分线与BC和圆O分别交于点D和E．（Ⅰ）求证AB•PC=PA•AC
（Ⅱ）求AD•AE的值．
考点：与圆有关的比例线段
专题：直线与圆
分析：（1）由已知条件推导出△PAB∽△PCA，由此能够证明AB•PC=PA•AC．
（2）由切割线定理求出PC=40，BC=30，由已知条件条件推导出△ACE∽△ADB，由此能求出AD•AE的值．
（2）由切割线定理求出PC=40，BC=30，由已知条件条件推导出△ACE∽△ADB，由此能求出AD•AE的值．
解答：
（1）证明：∵PA为圆O的切线，
∴∠PAB=∠ACP，又∠P为公共角，
∴△PAB∽△PCA，
∴
=
，
∴AB•PC=PA•AC．…（4分）
（2）解：∵PA为圆O的切线，BC是过点O的割线，
∴PA2=PB•PC，
∴PC=40，BC=30，
又∵∠CAB=90°，∴AC2+AB2=BC2=900，
又由（1）知
=
=
，
∴AC=12
，AB=6
，
连接EC，则∠CAE=∠EAB，
∴△ACE∽△ADB，∴
=
，
∴AD•AE=AB•AC=6
×12
=360．（10分）
∴∠PAB=∠ACP，又∠P为公共角，
∴△PAB∽△PCA，
∴
| AB |
| AC |
| PA |
| PC |
∴AB•PC=PA•AC．…（4分）
（2）解：∵PA为圆O的切线，BC是过点O的割线，
∴PA2=PB•PC，
∴PC=40，BC=30，
又∵∠CAB=90°，∴AC2+AB2=BC2=900，
又由（1）知
| AB |
| AC |
| PA |
| PC |
| 1 |
| 2 |
∴AC=12
| 5 |
| 5 |
连接EC，则∠CAE=∠EAB，
∴△ACE∽△ADB，∴
| AB |
| AE |
| AD |
| AC |
∴AD•AE=AB•AC=6
| 5 |
| 5 |
点评：本题考查三角形相似的证明和应用，考查线段乘积的求法，是中档题，解题时要注意切割线定理的合理运用．
练习册系列答案
相关题目
下列命题错误的是（ ）
| A、“x=1”是“x2-3x+2=0”的充分不必要条件 |
| B、对于命题p：?x∈R，使得x2+x+1＜0；则?p：?x∈R，均有x2+x+1≥0 |
| C、命题“若m＞0，则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根，则m≤0” |
| D、命题“若xy=0，则x、y中至少有一个为零”的否定式“若xy≠0，则x、y都不为零” |