题目内容
8.设复数z满足(1+2i)•z=3(i为虚数单位),则复数z的实部为$\frac{3}{5}$.分析 把已知等式变形,然后利用复数代数形式的乘除运算化简得答案.
解答 解:由(1+2i)•z=3,得$z=\frac{3}{1+2i}=\frac{3(1-2i)}{(1+2i)(1-2i)}=\frac{3}{5}-\frac{6}{5}i$,
∴复数z的实部为$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
18.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=5,$\overrightarrow{a}$•$\overrightarrow{b}$=6,λ∈R,则|$\overrightarrow{a}$-λ$\overrightarrow{b}$|的取值范围是( )
| A. | [$\frac{5}{3}$,+∞) | B. | [$\frac{6}{5}$,+∞) | C. | [$\frac{8}{5}$,+∞) | D. | [1,4] |
19.已知全集U=R,函数y=ln(x-1)的定义域为M,集合N={x|x2-x<0},则下列结论正确的是( )
| A. | M∩N=N | B. | M∩(∁UN)=∅ | C. | M∪N=U | D. | M⊆(∁UN) |
13.已知复数z满足$(1-i)\overline z=5+i$,则z=( )
| A. | 2+3i | B. | 2-3i | C. | 3+2i | D. | 3-2i |
20.已知数列{an}是公比为2的等比数列,且4a1为am,an的等比中项,则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{25}{6}$ | D. | 不存在 |
18.下列说法正确的是( )
| A. | 函数y=2x2-x+1在(0,+∞)上是增函数 | |
| B. | 幂函数在(0,+∞)上都是增函数 | |
| C. | 函数y=log2(x+$\sqrt{{x}^{2}+1}$)既不是奇函数,也不是偶函数 | |
| D. | 已知f(x)是定义在R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b) |
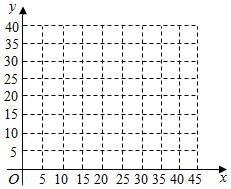 某公司为员工采购两年年终奖品,要求平板电脑的数量至多比手机多5部,预算经费12万,已知手机4千元一部,平板3千元一部,采购的手机和平板电脑的数量分别为x,y
某公司为员工采购两年年终奖品,要求平板电脑的数量至多比手机多5部,预算经费12万,已知手机4千元一部,平板3千元一部,采购的手机和平板电脑的数量分别为x,y