题目内容

17．设bn=$\frac{4}{（n+1）^{2}-1}$（n∈N*），求数列{bn}前n项和Tn．

分析 利用平方差公式可知（n+1）2-1=n（n+2），进而裂项可知bn=2（$\frac{1}{n}$-$\frac{1}{n+2}$）（n∈N*），并项相加即得结论．

解答 解：∵（n+1）2-1=n（n+2），
∴bn=$\frac{4}{（n+1）^{2}-1}$=2（$\frac{1}{n}$-$\frac{1}{n+2}$）（n∈N*），
∴Tn=2（1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$）
=2（1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$）
=3-$\frac{4n+6}{（n+1）（n+2）}$．

点评 本题考查数列的通项及前n项和，考查裂项相消法，注意解题方法的积累，属于中档题．

练习册系列答案
相关题目
7．已知函数f（x）=|x2-2x|+ax+a．
（1）当f（x）有两个零点时，求实数a的取值范围；
（2）当x∈R时，求函数的最小值g（a）．
8．设复数z满足（1+2i）•z=3（i为虚数单位），则复数z的实部为$\frac{3}{5}$．
5．已知f′（x）是函数f（x）=ln（1+x）的导函数，设g（x）=xf′（x），x≥0．
（1）证明：f（x）≥g（x）；
（2）令g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+，归纳并用数学归纳法证明gn（x）的表达式．
12．使函数y=sinx为增函数，且函数值为负数的区间是（　　）
A．（0，$\frac{π}{2}$）B．（$\frac{π}{2}$，π）C．（π，$\frac{3π}{2}$）D．（$\frac{3π}{2}$，2π）
2．设函数f（x）=$\sqrt{2x-2}$+$\sqrt{13-x}$的最大值为M．
（I）求两数f（x）的定义域和M的值；
（Ⅱ）是否存在实数x的值，使得|x-1|+|x+5|≤M？若存在，求出满足条件的x取值范围；若不存在，请说明理由．
9．已知函数f（x）=$\left\{\begin{array}{l}{sin（x+a），x≤0}\\{cos（x+b），x＞0}\end{array}\right.$是偶函数，则下列结论可能成立的是（　　）
A．a=$\frac{π}{4}$，b=-$\frac{π}{4}$B．a=$\frac{2π}{3}$，b=$\frac{π}{6}$C．a=$\frac{π}{3}$，b=$\frac{π}{6}$D．a=$\frac{5π}{6}$，b=$\frac{2π}{3}$
6．已知|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=8，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为150°．计算：
（1）（$\overrightarrow{a}$$+2\overrightarrow{b}$）•（2$\overrightarrow{a}$-$\overrightarrow{b}$）；
（2）|4$\overrightarrow{a}$-2$\overrightarrow{b}$|
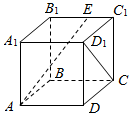9．如图，在正方体ABCD-A1B1C1D1中，E是线段B1C1上的动点，则异面直线AE与直线D1C所成的角为90°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网