题目内容
18.下列说法正确的是( )| A. | 函数y=2x2-x+1在(0,+∞)上是增函数 | |
| B. | 幂函数在(0,+∞)上都是增函数 | |
| C. | 函数y=log2(x+$\sqrt{{x}^{2}+1}$)既不是奇函数,也不是偶函数 | |
| D. | 已知f(x)是定义在R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b) |
分析 A,根据二次函数的图象与性质即可判断命题错误,
B,根据幂函数的图象与性质即可判断命题错误;
C,根据奇偶性的定义即可判断f(x)是定义域上的奇函数,原命题错误;
D,根据f(x)是定义在R上的增函数,且a+b>0,得出a>-b,f(a)>f(-b)与b>-a,f(b)>f(-a);两式相加即得结论.
解答 解:对于A,函数y=2x2-x+1的对称轴是x=$\frac{1}{4}$,在对称轴的两侧单调性相反,所以在(0,+∞)上是增函数,错误;
对于B,当α<0时,幂函数y=xα在(0,+∞)上是减函数,所以B错误;
对于C,函数y=log2(x+$\sqrt{{x}^{2}+1}$)的定义域为R,
且f(-x)=log2(-x+$\sqrt{{(-x)}^{2}+1}$)=log2$\frac{1}{x+\sqrt{{x}^{2}+1}}$=-log2(x+$\sqrt{{x}^{2}+1}$)=-f(x),
所以f(x)是定义域R上的奇函数,C错误;
对于D,f(x)是定义在R上的增函数,且a+b>0,
∴a>-b,f(a)>f(-b);
同理,-a<b,b>-a,
∴f(b)>f(-a);
∴f(a)+f(b)>f(-a)+f(-b),D正确.
故选:D.
点评 本题考查了幂函数、二次函数以及函数的奇偶性的应用问题,也考查了函数的单调性问题,是基础题目.

练习册系列答案
相关题目
9.已知函数f(x)=$\left\{\begin{array}{l}{sin(x+a),x≤0}\\{cos(x+b),x>0}\end{array}\right.$是偶函数,则下列结论可能成立的是( )
| A. | a=$\frac{π}{4}$,b=-$\frac{π}{4}$ | B. | a=$\frac{2π}{3}$,b=$\frac{π}{6}$ | C. | a=$\frac{π}{3}$,b=$\frac{π}{6}$ | D. | a=$\frac{5π}{6}$,b=$\frac{2π}{3}$ |
13.函数f(x)=tanωx(ω>0)的图象的相邻两支截直线y=1所得的线段长为$\frac{π}{4}$,则f($\frac{π}{12}$)的值是( )
| A. | 0 | B. | $\frac{\sqrt{3}}{3}$ | C. | 1 | D. | $\sqrt{3}$ |
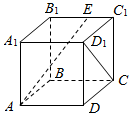 如图,在正方体ABCD-A1B1C1D1中,E是线段B1C1上的动点,则异面直线AE与直线D1C所成的角为90°.
如图,在正方体ABCD-A1B1C1D1中,E是线段B1C1上的动点,则异面直线AE与直线D1C所成的角为90°.