题目内容
16．
某公司为员工采购两年年终奖品，要求平板电脑的数量至多比手机多5部，预算经费12万，已知手机4千元一部，平板3千元一部，采购的手机和平板电脑的数量分别为x，y（Ⅰ）请列出x，y满足的数学关系式，并在所给的坐标系中画出相应的平面区域；
（Ⅱ）在上述条件下该公司最多采购多少部奖品．
分析 （ I）由题意写出不等式组$\left\{\begin{array}{l}{y-x≤5}\\{4x+3y≤120}\\{x，y∈N}\end{array}\right.$，从而作其可行域，
（ II）设采购奖品的总数为z，则z=x+y；从而利用线性规划求解．
解答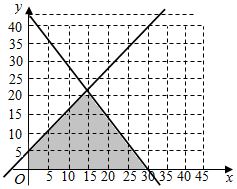 
解：（ I）由题意得，$\left\{\begin{array}{l}{y-x≤5}\\{4x+3y≤120}\\{x，y∈N}\end{array}\right.$，
作出其可行域如下，；
（ II）设采购奖品的总数为z，则z=x+y；
设直线l：x+y=0，由方程组$\left\{\begin{array}{l}{y-x=5}\\{4x+3y=120}\end{array}\right.$解得$\left\{\begin{array}{l}{x=15}\\{y=20}\end{array}\right.$；
平移直线l，可知目标函数z在点（15，20）处取到最大值，
故能采购的奖品最多为35部．其中15部手机，20部平板电脑．
点评 本题考查了线性规划在实际问题中的应用，同时考查了数形结合的思想方法的应用．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
1．设x∈（0，$\frac{1}{2}$），则“a∈（-∞，0）”是“log${\;}_{\frac{1}{2}}$x＞x+a”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不成分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |