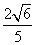题目内容
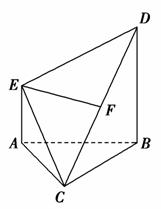
如图,已知矩形ABCD,PA⊥平面ABCD,M、N、R分别是AB、PC、CD的中点.求证:
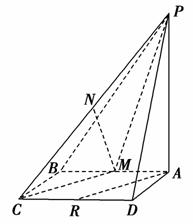
(1)直线AR∥平面PMC;
(2)直线MN⊥直线AB.
证法1:(1)连接CM,∵ABCD为矩形,R、M分别为AB、CD的中点,∴MA綊CR,∴AMCR为平行四边形,∴CM∥AR,
又∵AR⊄平面PMC,∴AR∥平面PMC.
(2)连接MR、NR,在矩形ABCD中,AB⊥AD,PA⊥平面AC,∴PA⊥AB,AB⊥平面PAD,∵MR∥AD,NR∥PD,
∴平面PDA∥平面NRM,
∴AB⊥平面NRM,则AB⊥MN.
证法2:(1)以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设AB=a,AD=b,AP=c,则B(a,0,0),D(0,b,0),P(0,0,c),C(a,b,0),∵M、N、P分别为AB、PC、CD的中点,∴M(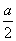 ,0,0),N(
,0,0),N(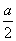 ,
, ,
,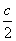 ),R(
),R(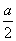 ,b,0),
,b,0),
 ∵AR⊄平面PMC,∴AR∥平面PMC.
∵AR⊄平面PMC,∴AR∥平面PMC.
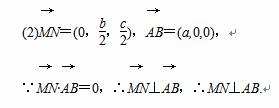

练习册系列答案
相关题目
 B.
B.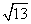 C.2
C.2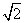 D.2
D.2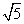
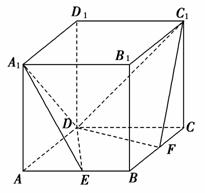
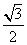 B.
B.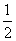
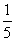 D.
D.