题目内容
过抛物线y2=8x的焦点F作倾斜角为135°的直线交抛物线于A、B两点,则弦AB的长为( )
A.4 B.8
C.12 D.16
D
[解析] 抛物线y2=8x的焦点F的坐标为(2,0),直线AB的倾斜角为135°,故直线AB的方程为y=-x+2,代入抛物线方程y2=8x,得x2-12x+4=0.设A(x1,y1),B(x2,y2),则弦AB的长|AB|=x1+x2+4=12+4=16.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
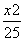 +
+ =1的位置关系为( )
=1的位置关系为( )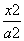 -
-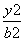 =1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P满足|PF2|=|F1F2|,且cos∠PF1F2=
=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P满足|PF2|=|F1F2|,且cos∠PF1F2=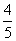 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( ) 与x轴正方向的夹角为60°,则△OAF的面积为( )
与x轴正方向的夹角为60°,则△OAF的面积为( )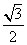 B.2
B.2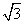 D.1
D.1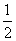 m后,水面的宽度是________m.
m后,水面的宽度是________m.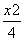 +
+ =1(0<b<2)的离心率等于
=1(0<b<2)的离心率等于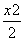 +y2=1短轴端点,且该双曲线的离心率与此椭圆的离心率之积为1,则该双曲线的方程为( )
+y2=1短轴端点,且该双曲线的离心率与此椭圆的离心率之积为1,则该双曲线的方程为( )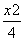 -y2=1 D.
-y2=1 D.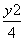 -x2=1
-x2=1
 B.75+4
B.75+4