题目内容
如图,在多面体ABCDE中,AE⊥平面ABC,DB∥AE,且AC=AB=BC=AE=1,BD=2,F为CD中点.
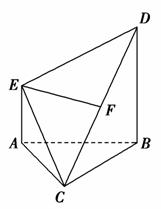
(1)求证:EF⊥平面BCD;
(2)求多面体ABCDE的体积;
(3)求平面ECD和平面ACB所成的锐二面角的余弦值.
(1)证明:取BC中点G,连接AG、FG,
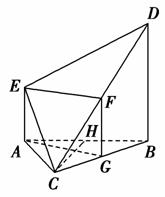
∵F、G分别为DC、BC中点,
∴FG綊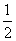 DB綊EA.
DB綊EA.
∴四边形EFGA为平行四边形.
∴EF∥AG.
∵AE⊥平面ABC,BD∥AE,
∴DB⊥平面ABC.
又∵DB⊂平面BCD,
∴平面ABC⊥平面BCD.
又∵G为BC中点且AC=AB=BC,
∴AG⊥BC.∴AG⊥平面BCD.∴EF⊥平面BCD.
(2)过C作CH⊥AB,则CH⊥平面ABDE且CH=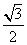 ,
,
∴VC-ABDE=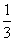 ×S四边形ABDE×CH=
×S四边形ABDE×CH=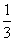 ×
×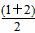 ×1×
×1×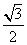 =
=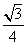 .
.
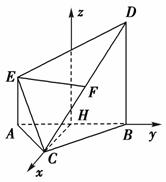
(3)过C作CH⊥AB于H,以H为原点建立如图所示的空间直角坐标系,
则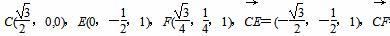 =(-
=(-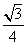 ,
,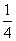 ,1),
,1),
设平面CEF的法向量为n=(x,y,z),
由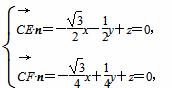
取n=(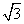 ,-1,1).
,-1,1).
又平面ABC的法向量为u=(0,0,1),
则cos〈n,u〉=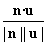 =
=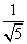 =
=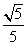 .
.
∴平面ECD和平面ACB所成的锐二面角的余弦值为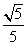 .
.

练习册系列答案
相关题目
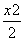 +y2=1短轴端点,且该双曲线的离心率与此椭圆的离心率之积为1,则该双曲线的方程为( )
+y2=1短轴端点,且该双曲线的离心率与此椭圆的离心率之积为1,则该双曲线的方程为( )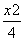 -y2=1 D.
-y2=1 D.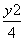 -x2=1
-x2=1 B.
B.
 D.
D.
 B.-
B.-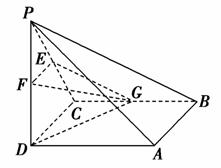
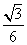 πa3 B.
πa3 B. πa3
πa3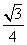 πa3 D.2
πa3 D.2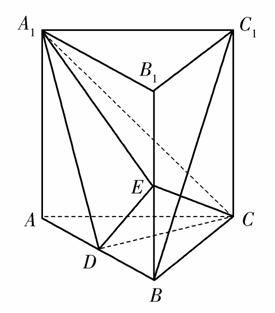
 ,求三棱锥C-A1DE的体积.
,求三棱锥C-A1DE的体积.