题目内容
2.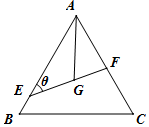 如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.
如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.(1)当$θ=\frac{π}{4}$时,求线段EG的长;
(2)当θ在区间$[\frac{π}{6},\frac{π}{2}]$上变化时,求$\frac{1}{EG}+\frac{1}{FG}$的取值范围.
分析 (1)由已知可求$∠EAG=\frac{π}{6}$,且$AG=2\sqrt{3}$,在△AEG中,由正弦定理即可解得EG的值.
(2)由正弦定理可求$EG=\frac{{\sqrt{3}}}{sinθ}$,$FG=\frac{{\sqrt{3}}}{{sin(\frac{2π}{3}-θ)}}$,利用三角函数恒等变换的应用化简可得$\frac{1}{EG}+\frac{1}{FG}$=$sin(θ+\frac{π}{6})$,求得范围$θ+\frac{π}{6}∈[\frac{π}{3},\frac{2π}{3}]$,利用正弦函数的性质即可计算得解.
解答  (本题满分为12分)
(本题满分为12分)
解:(1)由已知得$∠EAG=\frac{π}{6}$,且$AG=2\sqrt{3}$. …(2分)
在△AEG中,由正弦定理得$\frac{EG}{sin∠EAG}=\frac{AG}{sinθ}$,即$\frac{EG}{{sin\frac{π}{6}}}=\frac{{2\sqrt{3}}}{{sin\frac{π}{4}}}$,解得$EG=\sqrt{6}$. …(6分)
(2)在△AEG中,由正弦定理得$\frac{EG}{sin∠EAG}=\frac{AG}{sinθ}$,则$EG=\frac{{\sqrt{3}}}{sinθ}$,…(7分)
又$∠AFG=\frac{2π}{3}-θ$,同理可得$FG=\frac{{\sqrt{3}}}{{sin(\frac{2π}{3}-θ)}}$,…(8分)
可得:$\frac{1}{EG}+\frac{1}{FG}=\frac{1}{{\sqrt{3}}}[sinθ+sin(\frac{2π}{3}-θ)]=\frac{1}{{\sqrt{3}}}(\frac{3}{2}sinθ+\frac{{\sqrt{3}}}{2}cosθ)$=$sin(θ+\frac{π}{6})$,…(10分)
由$θ∈[\frac{π}{6},\frac{π}{2}]$,得$θ+\frac{π}{6}∈[\frac{π}{3},\frac{2π}{3}]$,则$sin(θ+\frac{π}{6})∈[\frac{{\sqrt{3}}}{2},1]$
即$\frac{1}{EG}+\frac{1}{FG}$的取值范围是$[\frac{{\sqrt{3}}}{2},1]$…(12分)
点评 本题主要考查了正弦定理,三角函数恒等变换的应用,正弦函数的图象和性质的综合应用,考查了转化思想和数形结合思想的应用,属于中档题.

| A. | 若x≠2,则x2-3x+2≠0 | B. | 若x2-3x+2=0,则x=2 | ||
| C. | 若x2-3x+2≠0,则x≠2 | D. | 若x=2,则x2-3x+2≠0 |
| A. | a>c>b | B. | b>c>a | C. | c>b>a | D. | c>a>b |
| A. | x3•x2=x5 | B. | x+x2=x3 | C. | 2x3÷x2=x | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
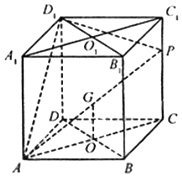 如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m
如图,在棱长为1的正方体中,P是侧棱CC1上的一点,CP=m