题目内容
17．已知圆O：x2+y2=r2（r＞0）与直线3x-4y+20=0相切，则r=4．分析 由圆的方程求出圆心坐标，直接用圆心到直线的距离等于半径求得答案．
解答 解：由x2+y2=r2，可知圆心坐标为（0，0），半径为r，
∵圆O：x2+y2=r2（r＞0）与直线3x-4y+20=0相切，
由圆心到直线的距离d=$\frac{20}{\sqrt{9+16}}$=4，
可得圆的半径为4．
故答案为：4．
点评 本题考查了直线和圆的位置关系，考查了点到直线的距离公式的应用，是基础题．
练习册系列答案
相关题目
7．已知直线y=-2x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）相交于A，B两点，且线段AB的中点在直线x-4y=0上，则此椭圆的离心率为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
5．
如图所示，O是坐标原点，两个正方形OABC、BDEF的顶点中，O、A、C、D、F五个点都在抛物线y2=2px（p＞0）上，另外，B、E两个点都在x轴上，若这两个正方形的面积之和为10，则（ ）
如图所示，O是坐标原点，两个正方形OABC、BDEF的顶点中，O、A、C、D、F五个点都在抛物线y2=2px（p＞0）上，另外，B、E两个点都在x轴上，若这两个正方形的面积之和为10，则（ ）| A． | p=1 | B． | p=2 | C． | p=$\frac{1}{2}$ | D． | p=$\sqrt{2}$ |
12．已知命题p：“?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是奇函数”，则命题?p为（ ）
| A． | ?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是偶函数 | B． | ?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$是奇函数 | ||
| C． | ?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$不是奇函数 | D． | ?m∈R，函数f（x）=m+$\frac{1}{{{2^x}+1}}$不是奇函数 |
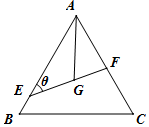如图所示，△ABC是边长为6的等边三角形，G是它的重心（三条中线的交点），过G的直线分别交线段AB、AC于E、F两点，∠AEG=θ．
如图，在直四棱柱（侧棱与底面垂直的四棱柱）ABCD-A1B1C1D1中，已知DC=DD1=2AD=2AB，AD⊥DC，AB∥DC，给出以下结论：