题目内容
7.下列运算中,正确的是( )| A. | x3•x2=x5 | B. | x+x2=x3 | C. | 2x3÷x2=x | D. | ($\frac{x}{2}$)3=$\frac{{x}^{3}}{2}$ |
分析 根据指数幂的运算性质计算即可
解答 解:对于A,根据同底数的运算法则可得,x3•x2=x5,故正确,
对于B:不是同类项,不能合并,故错误,
C:2x3÷x2=2x3-2=2x,故错误,
D,($\frac{x}{2}$)3=$\frac{{x}^{3}}{8}$,故错误,
故选:A
点评 本题考查了指数幂的运算性质,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.一次考试中,5名学生的数学、物理成绩如下:
求y关于x的线性回归方程.
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
19.为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:
已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
(1)请将上面的列表补充完整;
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由.
16.先后抛掷一枚硬币,出现“一次正面,一次反面”的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
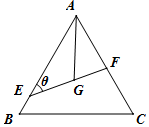 如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.
如图所示,△ABC是边长为6的等边三角形,G是它的重心(三条中线的交点),过G的直线分别交线段AB、AC于E、F两点,∠AEG=θ.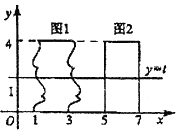 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处裁得两几何体的裁面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个矩形,且当实数t取[0,4]上的任意值时,直线y=t被图1和图2所截得的线段始终相等,则图1的面积为8.