题目内容
已知点P到点A(1,0),B(a,4)和到直线x=-1的距离都相等,如果这样的点P有且只有一个,那么实数a等于( )
| A、1 | B、2 |
| C、2或-2 | D、1或-1 |
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:由点P(x,y)到点A(1,0),到直线x=-1的距离都相等,可得P的轨迹是抛物线:y2=4x,且满足(x-a)2+(y-4)2=(x+1)2.把y2=4x代入第二个方程可得:
y2-8y+a2+15=0.(*)对a分类讨论,利用判别式与方程实数根的关系即可得出.
| 1-a |
| 2 |
解答:
解:由点P(x,y)到点A(1,0),到直线x=-1的距离都相等,
则P的轨迹是抛物线:y2=4x,且满足(x-a)2+(y-4)2=(x+1)2.
把y2=4x代入第二个方程可得:
y2-8y+a2+15=0.(*)
要使满足条件的点P有且只有一个.
a=1,(*)化为y=2,代入抛物线方程x=1,可得p(1,2)只有一个,满足条件.
当a≠1时,(*)只有一解,则△=0,化为(a+1)(a2-2a+17)=0,解得a=-1.
综上可得:a=-1或1.
故选:D.
则P的轨迹是抛物线:y2=4x,且满足(x-a)2+(y-4)2=(x+1)2.
把y2=4x代入第二个方程可得:
| 1-a |
| 2 |
要使满足条件的点P有且只有一个.
a=1,(*)化为y=2,代入抛物线方程x=1,可得p(1,2)只有一个,满足条件.
当a≠1时,(*)只有一解,则△=0,化为(a+1)(a2-2a+17)=0,解得a=-1.
综上可得:a=-1或1.
故选:D.
点评:本题考查了两点之间的距离公式、抛物线的定义、一元二次方程有实数根与判别式的关系,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
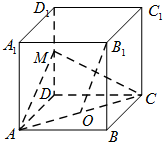 在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.
在正方体ABCD-A1B1C1D1中,M,O分别为DD1,AC的中点,AB=2.