题目内容
若f(x)=1+2cosx-cos2x,求函数f(x)的最大值与最小值.
考点:二倍角的余弦,复合三角函数的单调性
专题:三角函数的图像与性质
分析:利用余弦函数的倍角公式进行化简即可.
解答:
解:f(x)=1+2cosx-cos2x=f(x)=1+2cosx-(2cos2x-1)=-2cos2x+2cosx+2=-2(cosx-
)2+
,
∵-1≤cosx≤-1,
∴当cosx=
时,函数取得最大值
,
当cosx=-1时,函数取得最小值-2.
| 1 |
| 2 |
| 5 |
| 2 |
∵-1≤cosx≤-1,
∴当cosx=
| 1 |
| 2 |
| 5 |
| 2 |
当cosx=-1时,函数取得最小值-2.
点评:本题主要考查三角函数最值的求解,利用余弦函数的倍角公式结合一元二次函数的性质是解决本题的关键.

练习册系列答案
相关题目
已知点P到点A(1,0),B(a,4)和到直线x=-1的距离都相等,如果这样的点P有且只有一个,那么实数a等于( )
| A、1 | B、2 |
| C、2或-2 | D、1或-1 |
不等式2x-y-6>0表示的平面区域在直线2x-y-6=0的( )
| A、右上方 | B、左上方 |
| C、右下方 | D、左下方 |
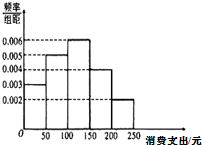 已知100名学生某月饮料消费支出情况的频率分布直方图如图所示.则这100名学生中,该月饮料消费支出超过150元的人数是
已知100名学生某月饮料消费支出情况的频率分布直方图如图所示.则这100名学生中,该月饮料消费支出超过150元的人数是