题目内容
已知函数f(x)=log2(x2-ax+3a)在[2,+∞)上是增函数,则实数a的取值范围是 .
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据复合函数的单调性函数x2-ax+3a在[2,+∞)是增函数,且x2-ax+3a>0,所以根据二次函数的单调性及最小值便有
,解该不等式组即得a的取值范围.
|
解答:
解:设g(x)=x2-ax+3a,根据对数函数及复合函数的单调性知:
g(x)在[2,+∞)上是增函数,且g(2)>0;
∴
;
∴-4<a≤4;
∴实数a的取值范围是(-4,4].
故答案为:(-4,4].
g(x)在[2,+∞)上是增函数,且g(2)>0;
∴
|
∴-4<a≤4;
∴实数a的取值范围是(-4,4].
故答案为:(-4,4].
点评:考查复合函数的单调性,二次函数的单调性及最小值,以及对数函数的单调性及定义域.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知点P到点A(1,0),B(a,4)和到直线x=-1的距离都相等,如果这样的点P有且只有一个,那么实数a等于( )
| A、1 | B、2 |
| C、2或-2 | D、1或-1 |
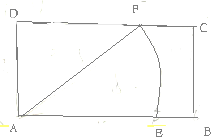 如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}
如图,矩形ABCD两邻边长分别为AB=6,AD=3,以A为圆心,5为半径画圆交AB于E,交CD于F,定义点集I={P|AP≤5}