题目内容
已知球的半径为R,一个圆锥的高等于这个球的直径,而且球的表面积等于圆锥的表面积,求圆锥的内接等边圆柱的体积.
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据球的半径为R,一个圆锥的高等于这个球的直径,而且球的表面积等于圆锥的表面积,求出圆锥的母线长和底面半径,进而求出圆锥的内接等边圆柱的底面半径和高,代入圆柱体积公式,可得答案.
解答:
解:半径为R的球的表面积为:4πR2,
设圆锥的底面边长为r,
由圆锥的高等于这个球的直径可得:
圆锥的母线l=
,
由球的表面积等于圆锥的表面积,
可得:πr(r+l)=πr(r+
)=4πR2,
解得:r2=
R2,即r=
R,
则l=
R,
故圆锥的轴截面为一个等边三角形,
设圆锥的内接等边圆柱的底面半径为r′,
则圆锥的内接等边圆柱的高为2r′,
则r′=(2
-3)r=(2
-3)
R=(4-2
)R,
则圆锥的内接等边圆柱的高为(8-4
)R,
故圆锥的内接等边圆柱的体积V=π•(r′)2•2r′=(416-240
)πR3
设圆锥的底面边长为r,
由圆锥的高等于这个球的直径可得:
圆锥的母线l=
| r2+4R2 |
由球的表面积等于圆锥的表面积,
可得:πr(r+l)=πr(r+
| r2+4R2 |
解得:r2=
| 4 |
| 3 |
| 2 |
| 3 |
| 3 |
则l=
| 4 |
| 3 |
| 3 |
故圆锥的轴截面为一个等边三角形,
设圆锥的内接等边圆柱的底面半径为r′,
则圆锥的内接等边圆柱的高为2r′,
则r′=(2
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
则圆锥的内接等边圆柱的高为(8-4
| 3 |
故圆锥的内接等边圆柱的体积V=π•(r′)2•2r′=(416-240
| 3 |
点评:本题考查的知识点是旋转体,熟练掌握圆锥的表面积公式,球的表面积公式及圆柱的体积公式,是解答的关键.

练习册系列答案
相关题目
已知点P到点A(1,0),B(a,4)和到直线x=-1的距离都相等,如果这样的点P有且只有一个,那么实数a等于( )
| A、1 | B、2 |
| C、2或-2 | D、1或-1 |
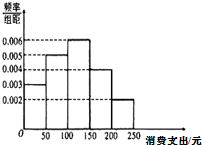 已知100名学生某月饮料消费支出情况的频率分布直方图如图所示.则这100名学生中,该月饮料消费支出超过150元的人数是
已知100名学生某月饮料消费支出情况的频率分布直方图如图所示.则这100名学生中,该月饮料消费支出超过150元的人数是 已知抛物线y2=4x的焦点为F,过点F作一条直线l与抛物线交于A(x1,y1),B(x2,y2)两点
已知抛物线y2=4x的焦点为F,过点F作一条直线l与抛物线交于A(x1,y1),B(x2,y2)两点