题目内容
若函数f(x)同时满足:①对于定义域上的任意x,恒有f(x)+f(-x)=0;②对于定义域上的任意x1,x2,当x1≠x2时,恒有
<0,则称函数f(x)为“理想函数”.
给出下列四个函数中:
(1)f(x)=x+1;
(2)f(x)=x2;
(3)f(x)=-x;
(4)f(x)=
,
能被称为“理想函数”的有 (填相应的序号).
| f(x1)-(x2) |
| x1-x2 |
给出下列四个函数中:
(1)f(x)=x+1;
(2)f(x)=x2;
(3)f(x)=-x;
(4)f(x)=
|
能被称为“理想函数”的有
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:新定义
分析:由“理想函数”的定义可知:若f(x)是“理想函数”,则f(x)为定义域上的单调递减的奇函数.
解答:
解:若f(x)是“理想函数”,则满足以下两条:
①对于定义域上的任意x,恒有f(x)+f(-x)=0,即f(-x)=-f(x),表明函数f(x)是奇函数;
②对于定义域上的任意x1,x2,当x1≠x2时,恒有
<0,即(x1-x2)(f(x1)-f(x2))<0,∴x1-x2与f(x1)-f(x2)异号,即函数f(x)是单调递减函数.即f(x)为定义域上的单调递减的奇函数.
据此可判断出:
(1)由f(x)=x+1单调递增,因此不是“理想函数”;
(2)f(x)=x2不是奇函数,因此不是“理想函数”;
(3)f(x)=-x,在R上既是奇函数,又是单调递减函数,因此是“理想函数”;
(4)f(x)=
,在R上既是奇函数,又是单调递减函数,因此是“理想函数”.
综上可知:能被称为“理想函数”的只有(3)(4).
故答案为:(3)(4).
①对于定义域上的任意x,恒有f(x)+f(-x)=0,即f(-x)=-f(x),表明函数f(x)是奇函数;
②对于定义域上的任意x1,x2,当x1≠x2时,恒有
| f(x1)-(x2) |
| x1-x2 |
据此可判断出:
(1)由f(x)=x+1单调递增,因此不是“理想函数”;
(2)f(x)=x2不是奇函数,因此不是“理想函数”;
(3)f(x)=-x,在R上既是奇函数,又是单调递减函数,因此是“理想函数”;
(4)f(x)=
|
综上可知:能被称为“理想函数”的只有(3)(4).
故答案为:(3)(4).
点评:本题考查了新定义、函数的奇偶性、单调性,属于中档题.

练习册系列答案
相关题目
已知a,b均为正实数,定义a?b=a(a-b),若x?2013=2014,则x的值为( )
| A、1 | B、2013 |
| C、2014 | D、-1或2014 |
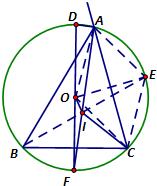 如图,设O,I分别为△ABC的外心、内心,且∠B=60°,AB>BC,∠A的外角平分线交⊙O于D,已知AD=18,则OI=.
如图,设O,I分别为△ABC的外心、内心,且∠B=60°,AB>BC,∠A的外角平分线交⊙O于D,已知AD=18,则OI=.