Question

已知函数f（x）=x²+xsinx+cosx．
（1）求f（x）的最小值；
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，求a与b的值．
（3）若曲线y=f（x）与直线y=b 有两个不同的交点，求b的取值范围．

Answer 1

考点：导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程

专题：导数的综合应用

分析：（1）由已知中函数的解析式，求导后判断函数的单调性，进而可得f（x）的最小值；
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，则f′（a）=0，b=f（a），进而可得a与b的值；
（3）当b≤1时，曲线y=f（x）与直线y=b最多只有一个交点；若曲线y=f（x）与直线y=b 有两个不同的交点，则b＞1．

解答： 解：（1）由f（x）=x²+xsinx+cosx，
得f′（x）=2x+sinx+xcosx-sinx=x（2+cosx）．…（1分）
令f′（x）=0，得x=0．…（2分）
列表如下：
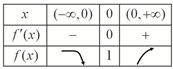  …（4分）
∴函数f（x）在区间（-∞，0）上单调递减，
在区间（0，+∞）上单调递增，
∴f（0）=1是f（x）的最小值．…（5分）
（2）∵曲线y=f（x）在点（a，f（a））处与直线y=b相切，
∴f′（a）=a（2+cosa）=0，b=f（a），…（7分）
解得a=0，b=f（0）=1．…（9分）
（3）当b≤1时，曲线y=f（x）与直线y=b最多只有一个交点；
当b＞1时，f（-2b）=f（2b）≥4b²-2b-1＞4b-2b-1＞b，f（0）=1＜b，
∴存在x₁∈（-2b，0），x₂∈（0，2b），使得f（x₁）=f（x₂）=b．…（12分）
由于函数f（x）在区间（-∞，0）和（0，+∞）上均单调，
∴当b＞1时曲线y=f（x）与直线y=b有且只有两个不同交点．…（13分）
综上可知，如果曲线y=f（x）与直线y=b有且只有两个不同交点，那么b取值范围是（1，+∞）．…（14分）

点评：本题考查的知识点是导数在最大值、最小值问题中的应用，导数法研究曲线的切线，是导数较为综合的应用，难度中档．