题目内容
给出如下四个命题:
①若“p∧q”为假命题,则p,q均为假命题;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“?x∈R,x2+1≥1”的否定是“?x0∈R,x02+1≤1”
④给出四个函数y=x-1,y=x,y=x2,y=x3,则在R上是增函数的有3个.
其中不正确的命题个数是( )
①若“p∧q”为假命题,则p,q均为假命题;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
③“?x∈R,x2+1≥1”的否定是“?x0∈R,x02+1≤1”
④给出四个函数y=x-1,y=x,y=x2,y=x3,则在R上是增函数的有3个.
其中不正确的命题个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①利用复合命题真值表可知①错误;
②利用命题“若p则q”的否命题为“若¬p则¬q”可判断②的正误;
③利用“?x∈R,p”之否定为“?x0∈R,¬p”,可判断③的正误;
④依题意,可知四个函数y=x-1,y=x,y=x2,y=x3,则在R上是增函数的有y=x与y=x3,从而可知④之正误.
②利用命题“若p则q”的否命题为“若¬p则¬q”可判断②的正误;
③利用“?x∈R,p”之否定为“?x0∈R,¬p”,可判断③的正误;
④依题意,可知四个函数y=x-1,y=x,y=x2,y=x3,则在R上是增函数的有y=x与y=x3,从而可知④之正误.
解答:
解:①若“p∧q”为假命题,则p,q中至少一个为假命题,故①错误;
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”正确;
③“?x∈R,x2+1≥1”的否定是“?x0∈R,x02+1<1”,故③错误;
④四个函数y=x-1,y=x,y=x2,y=x3,则在R上是增函数的有y=x与y=x3,共2个,故④错误;
综上所述,不正确的命题个数是3个,
故选:B.
②命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”正确;
③“?x∈R,x2+1≥1”的否定是“?x0∈R,x02+1<1”,故③错误;
④四个函数y=x-1,y=x,y=x2,y=x3,则在R上是增函数的有y=x与y=x3,共2个,故④错误;
综上所述,不正确的命题个数是3个,
故选:B.
点评:本题考查命题的真假判断与应用,考查复合命题的真假判断,掌握四种命题间的关系,否命题与命题的否定的区别及其真假判断是关键,属于中档题.

练习册系列答案
相关题目
设实数x,y满足不等式组
,则
的取值范围是( )
|
| y |
| x+3 |
A、[0,
| ||||
B、[
| ||||
C、[0,
| ||||
D、[
|
执行所示的程序框图,如果输入a=3,那么输出的n的值为( )


| A、2 | B、3 | C、4 | D、5 |
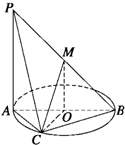 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题: 如图,在平面直角坐标系xOy中,椭圆C:
如图,在平面直角坐标系xOy中,椭圆C: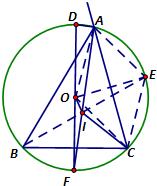 如图,设O,I分别为△ABC的外心、内心,且∠B=60°,AB>BC,∠A的外角平分线交⊙O于D,已知AD=18,则OI=.
如图,设O,I分别为△ABC的外心、内心,且∠B=60°,AB>BC,∠A的外角平分线交⊙O于D,已知AD=18,则OI=.