题目内容
求由约束条件
确定的平面区域的面积S和目标函数z=4x+3y的最大值.
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据对应图形,即可求出面积,利用z的几何意义利用数形结合即可得到结论.
解答:
 解:由约束条件作出其所确定的平面区域(阴影部分),其四个顶点为O(0,0),B(3,0),A(0,5),P(1,4).
解:由约束条件作出其所确定的平面区域(阴影部分),其四个顶点为O(0,0),B(3,0),A(0,5),P(1,4).
过P点作y轴的垂线,垂足为C.
则AC=|5-4|=1,PC=|1-0|=1,
OC=4,OB=3,AP=
,
PB=
=2
.
得S△ACP=
AC•PC=
,
S梯形COBP=
(CP+OB)•OC=8.
∴S=S△ACP+S梯形COBP=
.
平移直线z=4x+3y,由图象可知当直线z=4x+3y经过点P(1,4),
目标函数z=4x+3y取得最大值,最大值为16.
 解:由约束条件作出其所确定的平面区域(阴影部分),其四个顶点为O(0,0),B(3,0),A(0,5),P(1,4).
解:由约束条件作出其所确定的平面区域(阴影部分),其四个顶点为O(0,0),B(3,0),A(0,5),P(1,4).过P点作y轴的垂线,垂足为C.
则AC=|5-4|=1,PC=|1-0|=1,
OC=4,OB=3,AP=
| 2 |
PB=
| (4-0)2+(1-3)2 |
| 5 |
得S△ACP=
| 1 |
| 2 |
| 1 |
| 2 |
S梯形COBP=
| 1 |
| 2 |
∴S=S△ACP+S梯形COBP=
| 17 |
| 2 |
平移直线z=4x+3y,由图象可知当直线z=4x+3y经过点P(1,4),
目标函数z=4x+3y取得最大值,最大值为16.
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.要求熟练掌握常见目标函数的几何意义.

练习册系列答案
相关题目
执行所示的程序框图,如果输入a=3,那么输出的n的值为( )


| A、2 | B、3 | C、4 | D、5 |
 如图,已知P是矩形ABCD内任意一点,延长BP交AD于E,延长DP交AB于F,延长CP交矩形的外接圆于G.求证:GE⊥GF.
如图,已知P是矩形ABCD内任意一点,延长BP交AD于E,延长DP交AB于F,延长CP交矩形的外接圆于G.求证:GE⊥GF.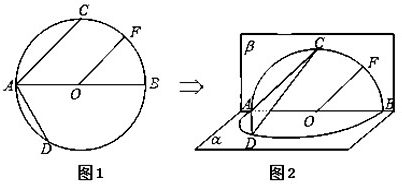
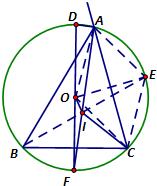 如图,设O,I分别为△ABC的外心、内心,且∠B=60°,AB>BC,∠A的外角平分线交⊙O于D,已知AD=18,则OI=.
如图,设O,I分别为△ABC的外心、内心,且∠B=60°,AB>BC,∠A的外角平分线交⊙O于D,已知AD=18,则OI=.