题目内容
5.若全集为实数集R,f(x)、g(x)均为x的二次函数,P={x|f(x)<0},Q={x|g(x)≤0},则不等式组$\left\{\begin{array}{l}f(x)<0\\ g(x)>0\end{array}\right.$的解集可用P、Q表示为P∩CIQ.分析 根据集合P与Q中的不等式,得到f(x)g(x)≤0,且f(x)≠0,即可确定出所求不等式组表示的意义.
解答 解:∵I=R,Q={x|g(x)≤0},
∴CIQ={x|g(x)>0},
∵P={x|f(x)<0},
则不等式组$\left\{\begin{array}{l}f(x)<0\\ g(x)>0\end{array}\right.$的解集可用P、Q表示为P∩CIQ.
故答案为:P∩CIQ
点评 此题考查了其他不等式的解法,以及补集、交集及其运算,弄清题意是解本题的关键.

练习册系列答案
相关题目
13.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°,且|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,则|$\overrightarrow{a}$-$\overrightarrow{b}$|等于( )
| A. | 1 | B. | $\sqrt{13}$ | C. | 13 | D. | $\sqrt{7-2\sqrt{3}}$ |
13.两个整数1908和4187的最大公约数是( )
| A. | 53 | B. | 43 | C. | 51 | D. | 67 |
15.判断函数f(x)=$\frac{{\sqrt{{x^2}+1}+x-1}}{{\sqrt{{x^2}+1}+x+1}}$的奇偶性( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
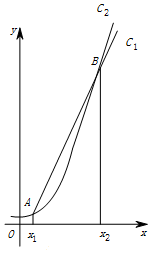 函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},则a+b=10.
函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},则a+b=10.