题目内容
已知函数f（x）=
x3+
x2+（a+b）x+c（a，b，c∈R）的两个极值点分别为x1，x2，且x1∈（0，1），x2∈（1，+∞），z=2a-b，则z的取值范围是（ ）
| 1 |
| 3 |
| a |
| 2 |
| A、（-∞，3] |
| B、（-∞，-3） |
| C、[-3，+∞） |
| D、（-3，+∞） |
考点：利用导数研究函数的极值
专题：导数的概念及应用,不等式的解法及应用
分析：对函数求导，由已知结合二次函数的图象可得
，代入可得关于a，b的二元一次不等式组，利用线性规划的知识，画出平面区域，在可行域内找到目标函数的取值范围．
|
解答：
解：∵函数f（x）=
x3+
x2+（a+b）x+c，
∴f′（x）=x2+ax+a+b
由题意可得f′（x）=0的两根x1，x2，
且x1∈（0，1），x2∈（1，+∞），
∴
，
满足条件的可行域如下图所示：
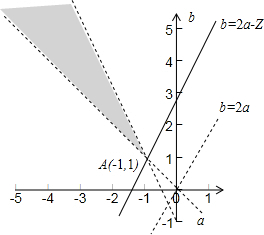
由图可知：当直线b=2a-Z过A（-1，1）时，Z取得最大值-3，Z无最小值，但由于不包括边界，
∴Z＜-3，
故z的取值范围是（-∞，-3），
故选：B
| 1 |
| 3 |
| a |
| 2 |
∴f′（x）=x2+ax+a+b
由题意可得f′（x）=0的两根x1，x2，
且x1∈（0，1），x2∈（1，+∞），
∴
|
满足条件的可行域如下图所示：
由图可知：当直线b=2a-Z过A（-1，1）时，Z取得最大值-3，Z无最小值，但由于不包括边界，
∴Z＜-3，
故z的取值范围是（-∞，-3），
故选：B
点评：本题以函数的极值为切入点，借助于二次函数的图象及二次方程的实根分布把问题转化为平面区域内求目标函数的最值问题，是一道综合性较好的试题，体会“转化思想”在解题中的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知在△ABC中，A为动点，B、C为定点，B（-
，0），C（
，0）（a＞0）且满足条件|sinC-sinB|=
sinA，则动点A的轨迹方程是（ ）
| a |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
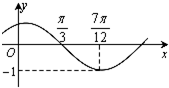函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|