题目内容
过抛物线x2=y焦点的直线l交抛物线于A、B两点,且|AB|=4,则线段AB中点到x轴的距离是( )
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:确定抛物线的准线方程,利用抛物线的定义及弦长,可得弦AB的中点到准线的距离,进而可求弦AB的中点到y轴的距离.
解答:
解:由题意,抛物线x2=y的焦点坐标为(0,
),
准线方程为y=-
,
根据抛物线的定义,
∵|AB|=4,
∴A、B到准线的距离和为4,
∴弦AB的中点到准线的距离为2
∴弦AB的中点到y轴的距离为2-
=
,
故选:C
| 1 |
| 4 |
准线方程为y=-
| 1 |
| 4 |
根据抛物线的定义,
∵|AB|=4,
∴A、B到准线的距离和为4,
∴弦AB的中点到准线的距离为2
∴弦AB的中点到y轴的距离为2-
| 1 |
| 4 |
| 7 |
| 4 |
故选:C
点评:本题考查抛物线的定义,考查学生的计算能力,正确运用抛物线的定义是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
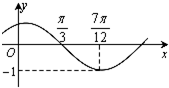 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知平面上三点A、B、C满足|
|=3,|
|=4,|
|=5,则
•
+
•
+
•
的值等于( )
| AB |
| BC |
| CA |
| AB |
| BC |
| BC |
| CA |
| CA |
| AB |
| A、25 | B、24 |
| C、-25 | D、-24 |
抛物线y2=4x的焦点坐标为( )
| A、(2,0) |
| B、(1,0) |
| C、(0,-4) |
| D、(-2,0) |
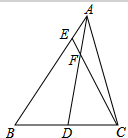 如图,在△ABC中,AD 是BC边上的中线,F是AD上的一点,且
如图,在△ABC中,AD 是BC边上的中线,F是AD上的一点,且