题目内容
设集合A={2,4,6,8,10},B={1,9,25,49,81,100},下面的对应关系能构成从A到B的映射的是( )
| A、f:x→(2x-1)2 |
| B、f:x→(2x-3)2 |
| C、f:x→x2-2x-1 |
| D、f:x→(x-1)2 |
考点:映射
专题:函数的性质及应用
分析:本题利用映射的定义判断选项中的对应关系能构成从A到B的映射,如不构成映射,可以举反例,正确的加以说明,即可得到本题结论.
解答:
解:根据映射的定义,对于集合A中的任一元素,集合B中有唯一的元素与之对应.
选项A,f:x→(2x-1)2,元素10∈A,(2×10-1)2=192=361∉B,不合题意;
选项B,f:x→(2x-3)2,元素10∈A,(2×10-3)2=192=289∉B,不合题意;
选项B,f:x→x2-2x-1,元素10∈A,102-2×10-1=179∉B,不合题意;
选项D,f:x→(x-1)2,
元素2∈A,(2-1)2=1∈B;
元素4∈A,(4-1)2=9∈B;
元素6∈A,(6-1)2=25∈B;
元素8∈A,(8-1)2=49∈B;
元素10∈A,(10-1)2=81∈B.
适合题意.
故选D.
选项A,f:x→(2x-1)2,元素10∈A,(2×10-1)2=192=361∉B,不合题意;
选项B,f:x→(2x-3)2,元素10∈A,(2×10-3)2=192=289∉B,不合题意;
选项B,f:x→x2-2x-1,元素10∈A,102-2×10-1=179∉B,不合题意;
选项D,f:x→(x-1)2,
元素2∈A,(2-1)2=1∈B;
元素4∈A,(4-1)2=9∈B;
元素6∈A,(6-1)2=25∈B;
元素8∈A,(8-1)2=49∈B;
元素10∈A,(10-1)2=81∈B.
适合题意.
故选D.
点评:本题考查了映射的概念,本题难度不大,属于基础题.

练习册系列答案
相关题目
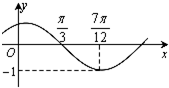 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|