题目内容
8.观察以下不等式:①1+$\frac{1}{2^2}$<$\frac{3}{2}$;
②1+$\frac{1}{2^2}$+$\frac{1}{3^2}$<$\frac{5}{3}$;
③1+$\frac{1}{2^2}$+$\frac{1}{3^2}$+$\frac{1}{4^2}$<$\frac{7}{4}$,
则第六个不等式是1+$\frac{1}{2^2}$+$\frac{1}{3^2}$+$\frac{1}{4^2}$+…+$\frac{1}{{7}^{2}}$<$\frac{13}{7}$.
分析 分析等式两边项数及分子、分母的变化规律,可得答案.
解答 解:由①1+$\frac{1}{2^2}$<$\frac{3}{2}$;
②1+$\frac{1}{2^2}$+$\frac{1}{3^2}$<$\frac{5}{3}$;
③1+$\frac{1}{2^2}$+$\frac{1}{3^2}$+$\frac{1}{4^2}$<$\frac{7}{4}$,
则第六个不等式是1+$\frac{1}{2^2}$+$\frac{1}{3^2}$+$\frac{1}{4^2}$+…+$\frac{1}{{7}^{2}}$<$\frac{13}{7}$,
故答案为1+$\frac{1}{2^2}$+$\frac{1}{3^2}$+$\frac{1}{4^2}$+…+$\frac{1}{{7}^{2}}$<$\frac{13}{7}$.
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
18.设集合M={x|x2=x},N={x|1<2x<2},则M∪N=( )
| A. | (-∞,2] | B. | (0,1] | C. | (0,2] | D. | [0,1] |
19.某校高三文科600名学生参加了12月的模拟考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,抽出的100名学生的数学、外语成绩如表:
(Ⅰ)若数学成绩优秀率为35%,求m,n的值;
(Ⅱ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(Ⅱ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
3.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+(4a-3)x+3a,x<0}\\{lo{g}_{a}(x+1)+1,x≥0}\end{array}\right.$(a>0且a≠1)在R上单调递减,则a的取值范围是( )
| A. | [$\frac{3}{4}$,1) | B. | (0,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{3}{4}$] | D. | (0,$\frac{1}{3}$] |
13.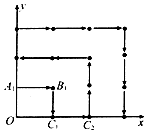 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
 某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )
某地区为了绿化环境进行大面积植树造林,如图所示,在区域{(x,y)|x≥0,y≥0}内植树,第1棵树在点A1(0,1)处,第2棵树在点B1(1,1)处,第3棵树在点C1(1,0)处,第4棵树在点C2(2,0)处,接着按图中箭头方向每隔1个单位种1棵树.第n棵树所在点的坐标是(46,0),则n=( )| A. | 1936 | B. | 2016 | C. | 2017 | D. | 2208 |
17.已知条件p:k=$-\sqrt{3}$;条件q:直线y=kx+2与圆x2+y2=1相切,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |